Option Strategies

Short Put Butterfly

Introduction

Short Put butterfly is the combination of a bull put spread and a bear put spread. In this strategy, all the puts have the same underlying stock, the same expiration date, and the strike price distance of ITM-ATM and OTM-ATM put pairs are the same. The short put butterfly strategy consists of selling an ITM put, selling an OTM put, and buying 2 ATM puts. This strategy profits from a drastic change in underlying price.

Implementation

Follow these steps to implement the short put butterfly strategy:

  1. In the Initializeinitialize method, set the start date, end date, cash, and Option universe.
    2. private Symbol _symbol;

public override void Initialize()
{
    SetStartDate(2024, 9, 1);
    SetEndDate(2024, 12, 31);
    SetCash(500000);

    UniverseSettings.Asynchronous = true;
    var option = AddOption("GOOG", Resolution.Minute);
    _symbol = option.Symbol;
    option.SetFilter(universe => universe.IncludeWeeklys().PutButterfly(30, 5));
}
    def initialize(self) -> None:
    self.set_start_date(2024, 9, 1)
    self.set_end_date(2024, 12, 31)
    self.set_cash(500000)

    self.universe_settings.asynchronous = True
    option = self.add_option("GOOG", Resolution.MINUTE)
    self._symbol = option.symbol
    option.set_filter(lambda universe: universe.include_weeklys().put_butterfly(30, 5))

    The PutButterflyput_butterfly filter narrows the universe down to just the three contracts you need to form a short put butterfly.

  2. In the OnDataon_data method, select the contracts of the strategy legs.
    3. public override void OnData(Slice slice)
{
    if (Portfolio.Invested ||
        !slice.OptionChains.TryGetValue(_symbol, out var chain))
    {
        return;
    }

    // Select the call Option contracts with the furthest expiry
    var expiry = chain.Max(x =x> x.Expiry);    
    var puts = chain.Where(x => x.Expiry == expiry && x.Right == OptionRight.Put);
    if (puts.Count() == 0) return;

    // Select the ATM, ITM and OTM contracts from the remaining contracts
    var atmPut = puts.OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price)).First();
    var itmPut = puts.OrderBy(x => x.Strike).SkipLast(1).Last();
    var otmPut = puts.Single(x => x.Strike == atmPut.Strike * 2 - itmPut.Strike);
    def on_data(self, slice: Slice) -> None:
    if self.portfolio.invested:
        return

    # Get the OptionChain
    chain = slice.option_chains.get(self._symbol, None)
    if not chain:
        return

    # Get the furthest expiry date of the contracts
    expiry = max([x.expiry for x in chain])
    
    # Select the call Option contracts with the furthest expiry
    puts = [i for i in chain if i.expiry == expiry and i.right == OptionRight.PUT]
    if len(puts) == 0:
        return

    # Select the ATM, ITM and OTM contracts from the remaining contracts
    atm_put = sorted(puts, key=lambda x: abs(x.strike - chain.underlying.price))[0]
    itm_put = sorted(puts, key=lambda x: x.strike)[-2]
    otm_put = [x for x in puts if x.strike == atm_put.strike * 2 - itm_put.strike][0]
  3. In the OnDataon_data method, place the orders.

    4. Approach A: Call the OptionStrategies.ShortButterflyPutOptionStrategies.short_butterfly_put method with the details of each leg and then pass the result to the Buybuy method.

    var optionStrategy = OptionStrategies.ShortButterflyPut(_symbol, itmPut.Strike, atmPut.Strike, otmPut.Strike, expiry);
Buy(optionStrategy, 1);
    option_strategy = OptionStrategies.short_butterfly_put(self._symbol, itm_put.strike, atm_put.strike, otm_put.strike, expiry)
self.buy(option_strategy, 1)

    Approach B: Create a list of Leg objects and then call the Combo Market Ordercombo_market_order, Combo Limit Ordercombo_limit_order, or Combo Leg Limit Ordercombo_leg_limit_order method.

    var legs = new List<Leg>()
    {
        Leg.Create(atmPut.Symbol, 2),
        Leg.Create(itmPut.Symbol, -1),
        Leg.Create(otmPut.Symbol, -1)
    };
ComboMarketOrder(legs, 1);
    legs = [
    Leg.create(atm_put.symbol, 2),
    Leg.create(itm_put.symbol, -1),
    Leg.create(otm_put.symbol, -1)
]
self.combo_market_order(legs, 1)

Strategy Payoff

The short put butterfly is a limited-reward-limited-risk strategy. The payoff is

$$ \begin{array}{rcll} P^{OTM}_T & = & (K^{OTM} - S_T)^{+}\\ P^{ITM}_T & = & (K^{ITM} - S_T)^{+}\\ P^{ATM}_T & = & (K^{ATM} - S_T)^{+}\\ P_T & = & (2\times P^{ATM}_T - P^{OTM}_T - P^{ITM}_T - 2\times P^{ATM}_0 + P^{ITM}_0 + P^{OTM}_0)\times m - fee \end{array} $$ $$ \begin{array}{rcll} \textrm{where} & P^{OTM}_T & = & \textrm{OTM put value at time T}\\ & P^{ITM}_T & = & \textrm{ITM put value at time T}\\ & P^{ATM}_T & = & \textrm{ATM put value at time T}\\ & S_T & = & \textrm{Underlying asset price at time T}\\ & K^{OTM} & = & \textrm{OTM put strike price}\\ & K^{ITM} & = & \textrm{ITM put strike price}\\ & K^{ATM} & = & \textrm{ATM put strike price}\\ & P_T & = & \textrm{Payout total at time T}\\ & P^{ITM}_0 & = & \textrm{ITM put value at position opening (credit received)}\\ & P^{OTM}_0 & = & \textrm{OTM put value at position opening (credit received)}\\ & P^{ATM}_0 & = & \textrm{ATM put value at position opening (debit paid)}\\ & m & = & \textrm{Contract multiplier}\\ & T & = & \textrm{Time of expiration} \end{array} $$

The following chart shows the payoff at expiration:

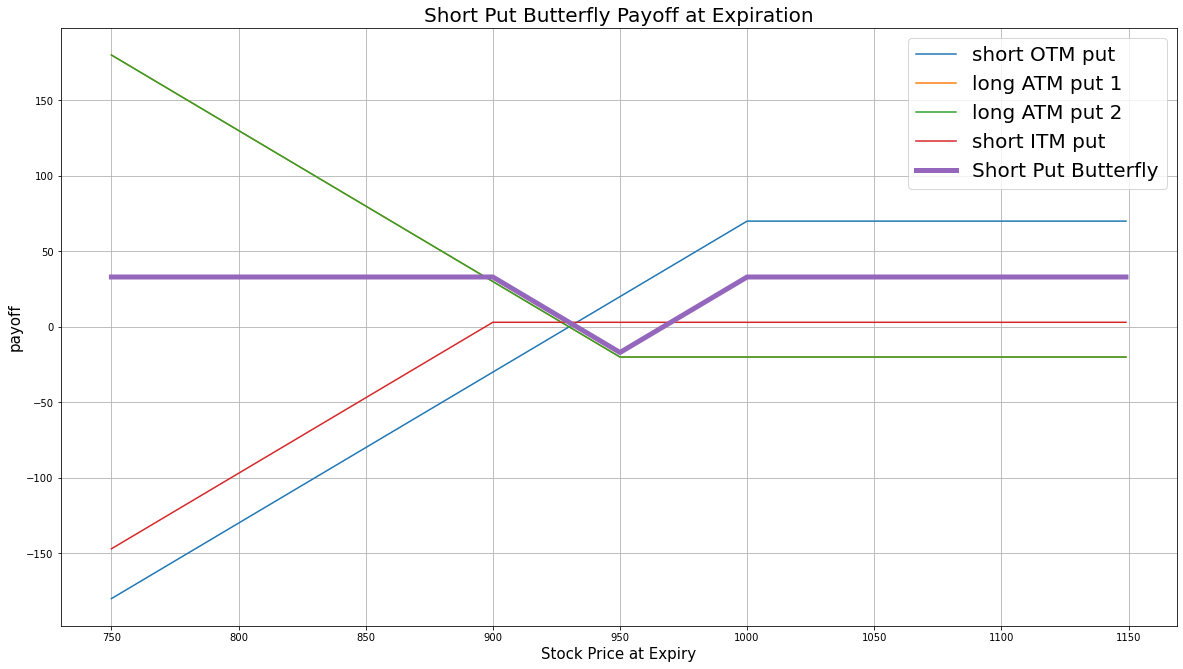
Strategy payoff decomposition and analysis of short put butterfly

The maximum profit is the net credit received, $P^{ITM}_0 + P^{OTM}_0 - 2\times P^{ATM}_0$. It occurs when the underlying price is below the ITM strike or above the OTM strike at expiration.

The maximum loss is $K^{ATM} - K^{OTM} - 2\times P^{ATM}_0 + P^{ITM}_0 + P^{OTM}_0$. It occurs when the underlying price at expiration is at the same price as when you opened the trade.

If the Option is American Option, there is a risk of early assignment on the contracts you sell.

Example

The following table shows the price details of the assets in the short put butterfly algorithm:

AssetPrice ($)Strike ($)
ITM put37.80832.50
ATM put14.70800.00
OTM put5.70767.50
Underlying Equity at expiration829.08-

Therefore, the payoff is

$$ \begin{array}{rcll} P^{OTM}_T & = & (K^{OTM} - S_T)^{+}\\ & = & (829.08-832.50)^{+}\\ & = & 0\\ P^{ITM}_T & = & (K^{ITM} - S_T)^{+}\\ & = & (829.08-767.50)^{+}\\ & = & 61.58\\ P^{ATM}_T & = & (K^{ATM} - S_T)^{+}\\ & = & (829.08-800.00)^{+}\\ & = & 29.08\\ P_T & = & (-P^{OTM}_T - P^{ITM}_T + 2\times P^{ATM}_T - 2\times P^{ATM}_0 + P^{ITM}_0 + P^{OTM}_0)\times m - fee\\ & = & (-61.58-0+29.08\times2+5.70+37.80-14.70\times2)\times100-1.00\times4\\ & = & 1064 \end{array} $$

So, the strategy gains $1,064.

The following algorithm implements a short put butterfly Option strategy:

public class BearPutSpreadStrategy : QCAlgorithm
{
    private Symbol _equity;
    private Symbol _symbol;

    public override void Initialize()
    {
        SetStartDate(2024, 9, 1);
        SetEndDate(2024, 12, 31);
        SetCash(100000);

        _equity = AddEquity("GOOG", Resolution.Minute).Symbol;
        var option = AddOption("GOOG", Resolution.Minute);
        _symbol = option.Symbol;
        option.SetFilter(universe => universe.IncludeWeeklys().PutButterfly(30, 5));
    }

    public override void OnData(Slice slice)
    {
        if (Portfolio.Invested) return;

        // Get the OptionChain of the symbol
        var chain = slice.OptionChains.get(_symbol, null);
        if (chain == null || chain.Count() == 0) return;

        // sorted the optionchain by expiration date and choose the furthest date
        var expiry = chain.OrderByDescending(x => x.Expiry).First().Expiry;
        
        // filter the put options from the contracts which expire on the furthest expiration date in the option chain.
        var puts = chain.Where(x => x.Expiry == expiry && x.Right == OptionRight.Put);
        if (puts.Count() == 0) return;

        // sort the put options with the same expiration date according to their strike price.
        var putStrikes = puts.Select(x => x.Strike).OrderBy(x => x);

        // get at-the-money strike
        var atmStrike = puts.OrderBy(x => Math.Abs(x.Strike - chain.Underlying.Price)).First().Strike;

        // Get the distance between lowest strike price and ATM strike, and highest strike price and ATM strike. 
        // Get the lower value as the spread distance as equidistance is needed for both side.
        var spread = Math.Min(Math.Abs(putStrikes.First() - atmStrike), Math.Abs(putStrikes.Last() - atmStrike));

        // select the strike prices for forming the option legs
        var itmStrike = atmStrike + spread;
        var otmStrike = atmStrike - spread;

        var optionStrategy = OptionStrategies.ShortButterflyPut(_symbol, itmStrike, atmStrike, otmStrike, expiry);
        // We open a position with 1 unit of the option strategy
        Buy(optionStrategy, 1);
    }
}
class PutButterflyStrategy(QCAlgorithm): 
    def initialize(self) -> None:
        self.set_start_date(2024, 9, 1)
        self.set_end_date(2024, 12, 31)
        self.set_cash(500000)

        option = self.add_option("GOOG", Resolution.MINUTE)
        self.symbol = option.symbol
        option.set_filter(self.universe_func)

    def universe_func(self, universe: OptionFilterUniverse) -> OptionFilterUniverse:
        return universe.include_weeklys().put_butterfly(30, 5)

    def on_data(self, data: Slice) -> None:
        # avoid extra orders
        if self.portfolio.invested: return

        # Get the OptionChain of the self.symbol
        chain = data.option_chains.get(self.symbol, None)
        if not chain: return

        # sorted the optionchain by expiration date and choose the furthest date
        expiry = sorted(chain, key = lambda x: x.expiry, reverse=True)[0].expiry
        
        # filter the put options from the contracts which expire on the furthest expiration date in the option chain.
        puts = [i for i in chain if i.expiry == expiry and i.right == OptionRight.PUT]
        if len(puts) == 0: return

        # sort the put options with the same expiration date according to their strike price.
        put_strikes = sorted([x.strike for x in puts])

        # get at-the-money strike
        atm_strike = sorted(puts, key=lambda x: abs(x.strike - chain.underlying.price))[0].strike

        # Get the distance between lowest strike price and ATM strike, and highest strike price and ATM strike. 
        # Get the lower value as the spread distance as equidistance is needed for both side.
        spread = min(abs(put_strikes[0] - atm_strike), abs(put_strikes[-1] - atm_strike))

        # select the strike prices for forming the option legs
        itm_strike = atm_strike + spread
        otm_strike = atm_strike - spread

        option_strategy = OptionStrategies.short_butterfly_put(self.symbol, itm_strike, atm_strike, otm_strike, expiry)
        # We open a position with 1 unit of the option strategy
        self.buy(option_strategy, 1)
        # self.sell(option_strategy, 1) if short put butterfly

Other Examples

For more examples, see the following algorithms:

Demonstration Algorithm
LongAndShortButterflyPutStrategiesAlgorithm.py Python LongAndShortButterflyPutStrategiesAlgorithm.cs C#

You can also see our Videos. You can also get in touch with us via Discord.

Did you find this page helpful?

Contribute to the documentation: