Slippage
Supported Models
Introduction
This page describes the pre-built slippage models in LEAN. If none of these models perform exactly how you want, create a custom slippage model.
Constant Model
The ConstantSlippageModel applies a constant percentage of slippage to each order. It's the default slippage model of the DefaultBrokerageModel.
security.SetSlippageModel(new ConstantSlippageModel(0));
security.SetSlippageModel(ConstantSlippageModel(0))
The following table describes the arguments the model accepts:
| Argument | Data Type | Description | Default Value |
|---|---|---|---|
slippagePercent | decimalfloat | The slippage percent for each order. The value must be in the interval (0, 1). |
To view the implementation of this model, see the LEAN GitHub repository.
Volume Share Model
The VolumeShareSlippageModel calculates the slippage of each order by multiplying the price impact constant by the square of the ratio of the order to the total volume. If the volume of the current bar is zero, the slippage percent is
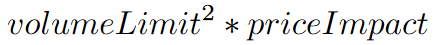
where volumeLimit and priceImpact are custom input variables. If the volume of the current bar is positive, the slippage percent is
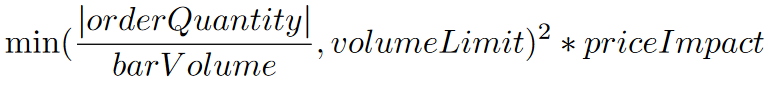
where orderQuantity is the quantity of the order and barVolume is the volume of the current bar. If the security subscription provides TradeBar data, the barVolume is the volume of the current bar. If the security subscription provides QuoteBar data, the barVolume is the bid or ask size of the current bar. CFD, Forex, and Crypto data often doesn't include volume. If there is no volume reported for these asset classes, the model returns zero slippage.
security.SetSlippageModel(new VolumeShareSlippageModel());
security.SetSlippageModel(VolumeShareSlippageModel())
The following table describes the arguments the model accepts:
| Argument | Data Type | Description | Default Value |
|---|---|---|---|
volumeLimit | decimalfloat | Maximum percent of historical volume that can fill in each bar. 0.5 means 50% of historical volume. 1.0 means 100%. | 0.025 |
priceImpact | decimalfloat | Scaling coefficient for price impact. Larger values will result in more simulated price impact. Smaller values will result in less simulated price impact. | 0.1 |
To view the implementation of this model, see the LEAN GitHub repository.
You can also see our Videos. You can also get in touch with us via Discord.
Did you find this page helpful?
