Popular Libraries

Import the copula, scipy, and sklearn libraries.

from AlgorithmImports import *
from copulas.bivariate import Bivariate
from scipy import stats
from sklearn.preprocessing import MinMaxScaler
import joblib

You need the joblib library to store models.

In the Initializeinitialize method, subscribe to some data so you can train the copula model and make predictions.

Since the algorithm is trading on options as speculation tools, to avoid insufficient buying power limited at the algorithm level, use NullBuyingPowerModel to bypass that.

def initialize(self) -> None:
    # Request spx and ndx data for option pricing and selection.
    self.spx = self.add_index("SPX", Resolution.DAILY).symbol
    self.ndx = self.add_index("NDX", Resolution.DAILY).symbol

    self.set_security_initializer(self.custom_security_initializer)

def custom_security_initializer(self, security: Security) -> None:
    # Seed the last price for the initial filtering on option contracts using the price data.
    security.set_market_price(self.get_last_known_price(security))
    # Allow infinite margin to start the option positions.
    security.set_buying_power_model(NullBuyingPowerModel())

In this example, build a copula model to estimate the log-return bivariate distribution of the paired securities, such that it can predict the correlated future price movement more accurately.

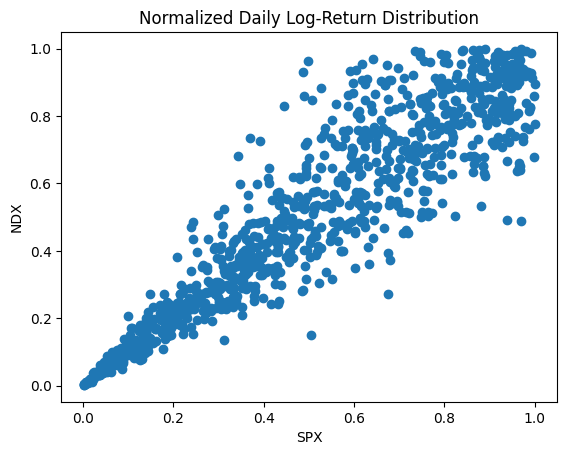
The following image shows the 1-year daily log-return bivariate distribution (normalized) of SPX and NDX indices as an example. As shown in the plot, although they exhibit a certain level of correlation, the tail is fat in both side, making normal distribution assumption unsuitable. In such case, we can make use of distributions from the extreme value theorem (Frank, Gumbel, or Clayton).

Follow the below steps to build the model:

1. Create a helper class to handle the copula trading.

class CopulaTrader:
    copula = None
    copula_name = None
    security1_scaler = MinMaxScaler()
    security2_scaler = MinMaxScaler()
    traded_pairs = []
    
    def __init__(self, algorithm: QCAlgorithm, security1: Symbol, security2: Symbol, alpha: float = 0.05, misprice_threshold: float = 2.5) -> None:
        self._algorithm = algorithm
        # Interest rate and dividend yield providers to calculate fair option price later.
        self.interest_rate_provider = algorithm.risk_free_interest_rate_model
        self.security1_dividend_yield_provider = DividendYieldProvider(security1)
        self.security2_dividend_yield_provider = DividendYieldProvider(security2)
        # The significance level on KS test of the copula goodness-of-fit
        self.alpha = alpha
        # The threshold of the price divergence of a mispriced pair to have in order to start the positions.
        # Should at least over the transaction fee with some margin.
        self.misprice_threshold = misprice_threshold

2. Create a method to transform the raw data into daily log-return, such that the series is more stationary while capturing sufficient variance to accurately estimate the bivariate distribution.

class CopulaTrader:
    copula = None
    copula_name = None
    security1_scaler = MinMaxScaler()
    security2_scaler = MinMaxScaler()

    def _data_preparation(self, security1_prices: np.ndarray, security2_prices: np.ndarray) -> np.ndarray:
        # Calculate log price difference for fitting copulas, since the series has more stationary domain for prediction.
        security1_log_price = np.log(security1_prices)
        security2_log_price = np.log(security2_prices)
        security1_log_diff = np.diff(security1_log_price)
        security2_log_diff = np.diff(security2_log_price)
        # Scale to [0, 1] to fit the model.
        scaled_security1_data = self.security1_scaler.fit_transform(security1_log_diff.reshape(-1, 1))
        scaled_security2_data = self.security2_scaler.fit_transform(security2_log_diff.reshape(-1, 1))
        data = np.column_stack((scaled_security1_data, scaled_security2_data))
        return data

3. Create a method to fit the copula with the distribution yielding the best log-likelihood.

def _fit_bivariate_copula(self, data: np.ndarray) -> None:
    # Select the best-fitted bivariate copula by log-likelihood.
    self.copula = Bivariate.select_copula(data)
    self.copula_name = self.copula.copula_type

4. (Optional) Reconfirm it by a 2-sample KS test.

def _fit_bivariate_copula(self, data: np.ndarray) -> None:
    # Continue from above

    # KS test to check if the actual data fits to the CDF of the copula good.
    samples = self.copula.sample(data.shape[0])
    p_value = self._ks2d2s(data[:, 0], samples[:, 0], data[:, 1], samples[:, 1])
    # Null hypothesis is the 2 datasets are having the same distribution, so if p < alpha, we reject the copula.
    if p_value < self.alpha:
        self.copula, self.copula_name = None, None
        self._algorithm.debug("No copula was fitted with statistically significant confidence.")
        return
    
    self._algorithm.debug(f"Best fitted copula distribution: {self.copula_name}, with tau: {self.copula.tau}")
    
def _ks2d2s(self, x1: np.ndarray, y1: np.ndarray, x2: np.ndarray, y2: np.ndarray) -> float:
    '''Two-dimensional Kolmogorov-Smirnov test on two samples. 
    Adapted from: https://github.com/syrte/ndtest/blob/master/ndtest.py'''
    def avgmaxdist(x1, y1, x2, y2):
        D1 = maxdist(x1, y1, x2, y2)
        D2 = maxdist(x2, y2, x1, y1)
        return (D1 + D2) / 2
    
    def maxdist(x1, y1, x2, y2):
        n1 = len(x1)
        D1 = np.empty((n1, 4))
        for i in range(n1):
            a1, b1, c1, d1 = quadct(x1[i], y1[i], x1, y1)
            a2, b2, c2, d2 = quadct(x1[i], y1[i], x2, y2)
            D1[i] = [a1 - a2, b1 - b2, c1 - c2, d1 - d2]
        
        D1[:, 0] -= 1 / n1

        dmin, dmax = -D1.min(), D1.max() + 1 / n1
        return max(dmin, dmax)

    def quadct(x, y, xx, yy):
        n = len(xx)
        ix1, ix2 = xx <= x, yy <= y
        a = np.sum(ix1 & ix2) / n
        b = np.sum(ix1 & ~ix2) / n
        c = np.sum(~ix1 & ix2) / n
        d = 1 - a - b - c
        return a, b, c, d
    
    n1, n2 = len(x1), len(x2)
    D = avgmaxdist(x1, y1, x2, y2)

    sqen = np.sqrt(n1 * n2 / (n1 + n2))
    r1 = stats.pearsonr(x1, y1)[0]
    r2 = stats.pearsonr(x2, y2)[0]
    r = np.sqrt(1 - 0.5 * (r1**2 + r2**2))
    d = D * sqen / (1 + r * (0.25 - 0.75 / sqen))
    p = stats.kstwobign.sf(d)
    
    return p

5. Instantiate the helper class and fit the copula model.

class CopulaTrader:
    def fit_bivariate_copula(self, security1_prices: np.ndarray, security2_prices: np.ndarray) -> None:
        training_data = self._data_preparation(security1_prices, security2_prices)
        self._fit_bivariate_copula(training_data)
            
class CopulaOptionTradingAlgorithm(QCAlgorithm):
    def initialize(self) -> None:
        # Set up the copula trading helper class.
        alpha = self.get_parameter("alpha", 0.05)
        misprice_threshold = self.get_parameter("misprice_threshold", 5)
        self.n_samples = self.get_parameter("n_samples", 1000)
        self.copula_trader = CopulaTrader(self, self.spx, self.ndx, alpha, misprice_threshold)
    
        # Fit the copula.
        # spx_prices & ndx_prices will be discussed later. They are 2 equal-size np array containing the raw price data of SPX and NDX.
        self.copula_trader.fit_bivariate_copula(spx_prices, ndx_prices)

You can train the model at the beginning of your algorithm and you can periodically re-train it as the algorithm executes.

Warm Up Training Data

You need historical data to initially train the model at the start of your algorithm. To get the initial training data, in the Initializeinitialize method, make a history request.

def initialize(self) -> None:
    # Create a rolling window to save the spx and ndx price for fitting the copula on their relationship.
    # We use the recent 1 year to fit the model.
    self.windows = {self.spx: RollingWindow[float](252), self.ndx: RollingWindow[float](252)}
    # Warm up the rolling windows with historical data for its immediate use.
    for bar in self.history[TradeBar](self.spx, 252, Resolution.DAILY):
        self.windows[self.spx].add(bar.close)
    for bar in self.history[TradeBar](self.ndx, 252, Resolution.DAILY):
        self.windows[self.ndx].add(bar.close)

Define a Training Method

To train the model, define a method that fits the model with the training data.

def fit_copula(self) -> None:
    # Obtain the historical price series of the spx and ndx for fitting the copula.
    # Note that we need to invert the rolling window series.
    spx_prices = np.array(list(self.windows[self.spx]))[::-1]
    ndx_prices = np.array(list(self.windows[self.ndx]))[::-1]
    # Fit the copula.
    self.copula_trader.fit_bivariate_copula(spx_prices, ndx_prices)

Set Training Schedule

To train the model at the beginning of your algorithm, in the Initializeinitialize method, call the Traintrain method.

# Fit the copula model for initial usage.
self.train(self.fit_copula)

To periodically re-train the model as your algorithm executes, in the Initializeinitialize method, call the Traintrain method as a Scheduled Event.

# Recalibrate the copula on every month to keep its accuracy updated.
self.train(self.date_rules.month_start(), self.time_rules.at(8,0), self.fit_copula)

Update Training Data

To update the training data as the algorithm executes, make use of a consolidator to automatically update the rolling windows when a daily bar is consolidated through a consolidator handler.

def initialize(self) -> None:
    # Set a daily consolidator to update the rolling windows automatically.
    self.consolidate(self.spx, Resolution.DAILY, lambda bar: self.windows[bar.symbol].add(bar.close))
    self.consolidate(self.ndx, Resolution.DAILY, lambda bar: self.windows[bar.symbol].add(bar.close))

In this example, we trade option mispricing arbitration using the copula model. More precisely, we are using the copula model to generate forward price series samples to price the options and do arbitration between options of the 2 correlated underlying. Since the copula can provide a distribution more accurately, we have an edge on the option pricing information.

Follow the below steps to trade the above logic:

1. Create a method to generate the forward price series samples of the 2 underlyings.

class CopulaTrader:
    def _get_simulated_paths(self, current_security1_price: float, current_security2_price: float, expiry: datetime, current: datetime, n_samples: int) -> Tuple[float, float]:
        # Get the year till expiry.
        dtm = (expiry - current).total_seconds() / 60 / 60 / 24
        
        future_log_prices = np.log(np.array([[[current_security1_price, current_security2_price]] * n_samples]))
        # Convert to estimated trading days left.
        for _ in range(int(dtm / 252 * 365)):
            # The future price is simulated from N stochastic simulations.
            future_log_diff = self.copula.sample(n_samples)
            # Convert the daily log-difference into future price.
            security1_log_diff = self.security1_scaler.inverse_transform(future_log_diff[:, 0].reshape(-1, 1))
            security2_log_diff = self.security2_scaler.inverse_transform(future_log_diff[:, 1].reshape(-1, 1))
            log_diff = np.column_stack((security1_log_diff, security2_log_diff))
            future_log_prices = np.concatenate([future_log_prices, np.array([future_log_prices[-1, :, :] + log_diff])], axis=0)
        
        self.paths = np.exp(future_log_prices)
        # Return the ultimate price at the last iteration, convert back to price from log-price.
        return self.paths[-1], dtm

2. Create a method to price the options through averaging the payoff over all simulated paths.

class CopulaTrader:
    def _calculate_fair_option_price(self, future_prices: np.ndarray, ttm: float, strike: float, right: OptionRight, interest_rate: float, dividend_yield: float, security2: bool = False) -> float:
        select_col = 1 if security2 else 0
        future_prices = future_prices[:, select_col]
        
        # Average of option payoffs among simulation paths. Make use of vectorize calculation here instead of util method.
        option_prices = np.maximum(future_prices - strike, 0) if right == OptionRight.CALL else np.maximum(strike - future_prices, 0)
        # Adjust the continuous dividend payoff yield and interest rate.
        return np.exp((dividend_yield - interest_rate) * ttm) * np.mean(option_prices)

3. Create a method to calculate the probability of winning (price converges to our model).

We use the ratio of paths that the underlyings ever reach the strikes of the options, since ATM options are most efficiently priced and equal among all option pricing engine.

class CopulaTrader:
    def _ratio_reached(self, data: np.ndarray, point: np.ndarray) -> float:
        # Count how many paths ever reached the point.
        count = 0
        for i in range(data.shape[1]):
            if point[0] <= max(data[:, i, 0]) and point[1] <= max(data[:, i, 1]) and point[0] >= min(data[:, i, 0]) and point[1] >= min(data[:, i, 1]):
                count += 1
        # Calculate the ratio of paths that the point has ever been reached.
        return count / data.shape[1]

4. Create a method to calculate the aboves and output the mispriced option pairs.

class CopulaTrader:
    def scan_option_mispricing_combinations(self, security1_options: List[OptionContract], security2_options: List[OptionContract], current_security1_price: float, current_security2_price: float,
        current: datetime, n_samples: int = 1000) -> List[Tuple[OptionContract, OptionContract, float, float]]:
        # Get the simluated price series till the expiry. Note that you should use single expiry for all contracts for easier handling and stable theta.
        future_prices, dtm = self._get_simulated_paths(current_security1_price, current_security2_price, security1_options[0].expiry, current, n_samples)
        
        mispriced_pairs = []
        interest_rate = self.interest_rate_provider.get_interest_rate(current)
        security1_dividend_yield = self.security1_dividend_yield_provider.get_dividend_yield(current)
        security2_dividend_yield = self.security2_dividend_yield_provider.get_dividend_yield(current)

        # Separate call and put options to avoid mixed right pairs, in order to keep theta close to 0.
        for right in [OptionRight.CALL, OptionRight.PUT]:
            sorted_security1_options = sorted([contract for contract in security1_options if contract.right == right], key=lambda x: x.strike)
            sorted_security2_options = sorted([contract for contract in security2_options if contract.right == right], key=lambda x: x.strike)
            ttm = dtm / 365

            # Calculate the security1-security2 fair prices and spot any significant mispricing.
            for i, security1_option in enumerate(sorted_security1_options):
                for j, security2_option in enumerate(sorted_security2_options):
                    # Skip the pairs already being traded.
                    if (security1_option.symbol, security2_option.symbol) in [(y.symbol for y in x[0]) for x in self.traded_pairs]:
                        continue
                    
                    # Calculate the probability of price converges. Since the ATM options are the most efficiently priced, we use that as a proxy for our win rate.
                    # The probability will be based on the whether the simulated paths have ever reached the point (so it was ever ATM).
                    prob = self._ratio_reached(self.paths, [security1_option.strike, security2_option.strike])

                    security1_price = self._calculate_fair_option_price(future_prices, ttm, security1_option.strike, right, interest_rate, security1_dividend_yield, False)
                    security2_price = self._calculate_fair_option_price(future_prices, ttm, security2_option.strike, right, interest_rate, security2_dividend_yield, True)
                    # Add to trade stacks only if the mispricing is opposite in direction and above profit threshold.
                    security1_price_divergence = security1_price - security1_option.ask_price
                    security2_price_divergence = security2_price - security2_option.bid_price
                    price_divergence1 = security1_price_divergence - security2_price_divergence
                    price_divergence2 = security1_price - security1_option.bid_price - security2_price + security2_option.ask_price
                    price_divergence = price_divergence1 if abs(price_divergence1) > abs(price_divergence2) else price_divergence1
                    if abs(price_divergence) > self.misprice_threshold and np.sign(security1_price_divergence) != np.sign(security2_price_divergence):
                        mispriced_pairs.append((security1_option, security2_option, price_divergence, prob))
        
        self._algorithm.debug(f"Found {len(mispriced_pairs)} mispriced option contract pairs.")

        return mispriced_pairs

5. Create a method to get the optimal position sizings for the top-expected-return trading opportnities.

class CopulaTrader:
    def trade_options(self, mispriced_pairs: List[Tuple[OptionContract, OptionContract, float, float]], fund: float, contract_multiplier: int = 100) -> Dict[OptionContract, int]:
        orders = {}
        total_pct = 0

        # Only trade on the top 10 expected return pairs.
        top_expected_ret = sorted(mispriced_pairs, key=lambda x: abs(x[2]) * x[3], reverse=True)[:10]
        for security1_option, security2_option, price_divergence, prob in top_expected_ret:
            # Calculate the order size of the mispricing pairs.
            contract1_price = security1_option.ask_price if price_divergence > 0 else security1_option.bid_price
            contract2_price = security2_option.ask_price if price_divergence < 0 else security2_option.bid_price
            security1_option_order_size, security2_option_order_size, order_pct = self._calculate_order_size(price_divergence, fund, prob, contract1_price, contract2_price, contract_multiplier)
            # Only order those with positive Kelly sizing and keep the exposure to cash only.
            # Keep 5% buffer to avoid order errors.
            if order_pct and total_pct + order_pct <= 0.95:
                if security1_option not in orders:
                    orders[security1_option] = 0
                if security2_option not in orders:
                    orders[security2_option] = 0
            # Aggregate the overall order sizes between all pairs.
                orders[security1_option] += security1_option_order_size
                orders[security2_option] += security2_option_order_size
                total_pct += order_pct
                self.traded_pairs.append(((security1_option, security2_option), (security1_option_order_size, security2_option_order_size)))

        return orders
            
    def _calculate_order_size(self, price_divergence: float, fund: float, prob_win: float, security1_option_price: float, security2_option_price: float, contract_multiplier: int) -> Tuple[int, int, float]:
        # The profit percentage is based on the option prices.
        capital = security1_option_price + security2_option_price
        profit_pct = abs(price_divergence) / capital
        # Assume no recovery at expiry if the price does not converges, while no extra loss will be paid.
        # To improve, you may use a continuous distribution to model the aggregated profit.
        # Keep at most 5% per trade, since option has leverage effect.
        order_pct = min(prob_win - (1 - prob_win) / profit_pct, 0.05)
        # The order size should be the shared by both side of the legs.
        order_size = order_pct * fund / capital // contract_multiplier
        order_pct = order_size * capital / fund
        # If the optimal order size is negative, do not place order.
        if order_pct < 0:
            return 0, 0, 0
        # If price divergence above 0, meaning security1 option is underpriced and the security2 option is overpriced, so we buy the security1 option and sell the security2 option.
        if price_divergence > 0:
            return order_size, -order_size, order_pct
        # Vice versa otherwise.
        return -order_size, order_size, order_pct

6. Create a method to handle the portfolio and exit the positions when price converges.

class CopulaTrader:
    def exit_trades(self, current: datetime) -> Dict[OptionContract, int]:
        # Get the parameters for fair price calculation.
        interest_rate = self.interest_rate_provider.get_interest_rate(current)
        security1_dividend_yield = self.security1_dividend_yield_provider.get_dividend_yield(current)
        security2_dividend_yield = self.security2_dividend_yield_provider.get_dividend_yield(current)

        exit_positions = {}
        for ((contract1, contract2), (size1, size2)) in self.traded_pairs.copy():
            # Get the simluated price series till the expiry.
            future_prices = self.paths[-1]
            ttm = (contract1.expiry - current).total_seconds() / 60 / 60 / 24 / 365
            # Check if the price discrepancy converges (relatively).
            contract1_price = self._calculate_fair_option_price(future_prices, ttm, contract1.strike, contract1.right, interest_rate, security1_dividend_yield, False)
            contract2_price = self._calculate_fair_option_price(future_prices, ttm, contract2.strike, contract2.right, interest_rate, security2_dividend_yield, True)
            contract1.mid_price = (contract1.bid_price + contract1.ask_price) * 0.5
            contract2.mid_price = (contract2.bid_price + contract2.ask_price) * 0.5
            contract1_divergence = contract1_price - contract1.mid_price
            contract2_divergence = contract2_price - contract2.mid_price
            price_divergence = contract1_divergence - contract2_divergence
            
            # If so, place the opposite size to exit the positions.
            if (size1 > 0 and price_divergence <= 0) or (size1 < 0 and price_divergence >= 0):
                if contract1 not in exit_positions:
                    exit_positions[contract1] = 0
                if contract2 not in exit_positions:
                    exit_positions[contract2] = 0
                exit_positions[contract1] -= size1
                exit_positions[contract2] -= size2
                # Remove the record and allow the pair to be traded again.
                self.traded_pairs.remove(((contract1, contract2), (size1, size2)))

        return exit_positions

7. Create a method in the base algorithm to open trades. Schedule its run.

To simply implementation, this example will only open trades after the previous positions are all expired, but you can change it to scan by some time interval.

class CopulaOptionTradingAlgorithm(QCAlgorithm):
    def open_trades(self) -> None:
        next_trading_day = self.securities[self.spx].exchange.hours.get_next_trading_day(self.time)
        
        if self.copula_trader.copula is not None:
            self.copula_trader.traded_pairs = []
            # Obtain the option chain of the spx and the ndx for trading.
            spx_options = self.option_chain(self.spx)
            ndx_options = self.option_chain(self.ndx)
            # Only use European options since the computation of averaging option payoff to price is more efficient.
            # Only include the ones within 5% of the current price, since they are more liquid and less susceptible from slippage.
            spx_price = self.securities[self.spx].price
            ndx_price = self.securities[self.ndx].price
            european_spx_options = [contract for contract in spx_options if contract.style == OptionStyle.EUROPEAN and spx_price * 1.05 > contract.strike > spx_price * 0.95]
            european_ndx_options = [contract for contract in ndx_options if contract.style == OptionStyle.EUROPEAN and ndx_price * 1.05 > contract.strike > ndx_price * 0.95]
            # Get the nearest expiry after 7 days to trade them. We use a single expiry to trade with more stable theta.
            expiry = min(set(contract.expiry for contract in european_spx_options if contract.expiry > self.time + timedelta(7)) \
                .intersection(set(contract.expiry for contract in european_ndx_options if contract.expiry > self.time + timedelta(7))))
            filtered_spx_options = [contract for contract in european_spx_options if contract.expiry == expiry]
            filtered_ndx_options = [contract for contract in european_ndx_options if contract.expiry == expiry]

            # Use simulations to price options by the fitted copula distributions to spot mispricing option pairs.
            mispriced_option_pairs = self.copula_trader.scan_option_mispricing_combinations(filtered_spx_options, filtered_ndx_options, spx_price, ndx_price, self.time, self.n_samples)
            # Obtain the trading plan from the mispriced options, calculated using Kelly Criterion.
            trade_plan = self.copula_trader.trade_options(mispriced_option_pairs, self.portfolio.cash, 100)
            # Order both plans. Request the option contract data to trade it.
            for contract, size in trade_plan.items():
                symbol = self.add_option_contract(contract).symbol
                self.market_order(symbol, size)

            next_trading_day = self.securities[self.spx].exchange.hours.get_next_trading_day(expiry)

        # Schedule the next option trades to be after the current selected expiry/today to simplify path calculation.
        self.schedule.on(
            self.date_rules.on(next_trading_day),
            self.time_rules.after_market_open(self.spx, 1), 
            self.open_trades
        )

8. Scan every N minutes to exit the positions if the price discrepancy between a pair is converged.

   class CopulaOptionTradingAlgorithm(QCAlgorithm):
       def on_data(self, slice: Slice) -> None:
           # Scan every 5 minutes to check price convergence.
           if slice.time.minute % 5 == 0:
               exit_plan = self.copula_trader.exit_trades(self.time)
               # Exit the paired positions when the price converges.
               for contract, size in exit_plan.items():
                   self.market_order(contract.symbol, size)

Follow these steps to save copula models into the Object Store:

1. Set the key name you want to store the model under in the Object Store.

# Set the storage key to something representative.
model_key = "copula"

2. Call the GetFilePathget_file_path method with the key.

# Get the file path to save and access the model in the Object Store.
file_name = self.object_store.get_file_path(model_key)

This method returns the file path where the model will be stored.

3. Call the dump method the file path.

# Serialize and save the model.
joblib.dump(self.predict, self.copula_trader.copula)

If you dump the model using the joblib module before you save the model, you don't need to retrain the model.

You can load and trade with pre-trained copula models that you saved in the Object Store. To load a copula model from the Object Store, in the Initializeinitialize method, get the file path to the saved model and then call the load method.

# Load the trained Aesera model from the Object Store.
def initialize(self) -> None:
    if self.object_store.contains_key(model_key):
        file_name = self.object_store.get_file_path(model_key)
        self.copula_trader.copula = joblib.load(file_name)

The ContainsKeycontains_key method returns a boolean that represents if the model_key is in the Object Store. If the Object Store does not contain the model_key, save the model using the model_key before you proceed.

The below demonstrates the full algorithm of the above example.

from AlgorithmImports import *
from copulas.bivariate import Bivariate
from scipy import stats
from sklearn.preprocessing import MinMaxScaler

class CopulaOptionTradingAlgorithm(QCAlgorithm):
    def initialize(self) -> None:
        self.set_start_date(2023, 1, 1)
        self.set_end_date(2023, 7, 1)
        self.set_cash(100000000)
        self.set_security_initializer(self.custom_security_initializer)

        # Request spx and ndx data for option pricing and selection.
        self.spx = self.add_index("SPX", Resolution.DAILY).symbol
        self.ndx = self.add_index("NDX", Resolution.DAILY).symbol

        # Set up the copula trading helper class.
        alpha = self.get_parameter("alpha", 0.05)
        misprice_threshold = self.get_parameter("misprice_threshold", 5)
        self.n_samples = self.get_parameter("n_samples", 1000)
        self.copula_trader = CopulaTrader(self, self.spx, self.ndx, alpha, misprice_threshold)

        # Create a rolling window to save the spx and ndx price for fitting the copula on their relationship.
        # We use the recent 1 year to fit the model.
        self.windows = {self.spx: RollingWindow[float](252), self.ndx: RollingWindow[float](252)}
        # Set a daily consolidator to update the rolling windows automatically.
        self.consolidate(self.spx, Resolution.DAILY, lambda bar: self.windows[bar.symbol].add(bar.close))
        self.consolidate(self.ndx, Resolution.DAILY, lambda bar: self.windows[bar.symbol].add(bar.close))
        # Warm up the rolling windows with historical data for its immediate use.
        for bar in self.history[TradeBar](self.spx, 252, Resolution.DAILY):
            self.windows[self.spx].add(bar.close)
        for bar in self.history[TradeBar](self.ndx, 252, Resolution.DAILY):
            self.windows[self.ndx].add(bar.close)

        # Fit the copula model for initial usage.
        self.train(self.fit_copula)
        # Recalibrate the copula on every month to keep its accuracy updated.
        self.train(self.date_rules.month_start(), self.time_rules.at(8,0), self.fit_copula)

        # Instantiate the next trade on the next market open.
        next_trading_day = self.securities[self.spx].exchange.hours.get_next_trading_day(self.time)
        self.schedule.on(
            self.date_rules.on(next_trading_day),
            self.time_rules.after_market_open(self.spx, 1), 
            self.open_trades
        )

    def custom_security_initializer(self, security: Security) -> None:
        # Seed the last price for the initial filtering on option contracts using the price data.
        security.set_market_price(self.get_last_known_price(security))
        # Allow infinite margin to start the option positions.
        security.set_buying_power_model(NullBuyingPowerModel())

    def fit_copula(self) -> None:
        # Obtain the historical price series of the spx and ndx for fitting the copula.
        # Note that we need to invert the rolling window series.
        spx_prices = np.array(list(self.windows[self.spx]))[::-1]
        ndx_prices = np.array(list(self.windows[self.ndx]))[::-1]
        # Fit the copula.
        self.copula_trader.fit_bivariate_copula(spx_prices, ndx_prices)

    def open_trades(self) -> None:
        # Obtain the option chain of the spx and the ndx for trading.
        spx_options = self.option_chain(self.spx)
        ndx_options = self.option_chain(self.ndx)
        # Only use European options since the computation of averaging option payoff to price is more efficient.
        # Only include the ones within 5% of the current price, since they are more liquid and less susceptible from slippage.
        spx_price = self.securities[self.spx].price
        ndx_price = self.securities[self.ndx].price
        european_spx_options = [contract for contract in spx_options if contract.style == OptionStyle.EUROPEAN and spx_price * 1.05 > contract.strike > spx_price * 0.95]
        european_ndx_options = [contract for contract in ndx_options if contract.style == OptionStyle.EUROPEAN and ndx_price * 1.05 > contract.strike > ndx_price * 0.95]
        # Get the nearest expiry after 7 days to trade them. We use a single expiry to trade with more stable theta.
        expiry = min(set(contract.expiry for contract in european_spx_options if contract.expiry > self.time + timedelta(7)) \
            .intersection(set(contract.expiry for contract in european_ndx_options if contract.expiry > self.time + timedelta(7))))
        filtered_spx_options = [contract for contract in european_spx_options if contract.expiry == expiry]
        filtered_ndx_options = [contract for contract in european_ndx_options if contract.expiry == expiry]

        # Use simulations to price options by the fitted copula distributions to spot mispricing option pairs.
        mispriced_option_pairs = self.copula_trader.scan_option_mispricing_combinations(filtered_spx_options, filtered_ndx_options, spx_price, ndx_price, self.time, self.n_samples)
        # Obtain the trading plan from the mispriced options, calculated using Kelly Criterion.
        trade_plan = self.copula_trader.trade_options(mispriced_option_pairs, self.portfolio.cash, 100)
        # Order both plans. Request the option contract data to trade it.
        for contract, size in trade_plan.items():
            symbol = self.add_option_contract(contract).symbol
            self.market_order(symbol, size)

        # Schedule the next option trades to be after the current selected expiry to simplify path calculation.
        next_trading_day = self.securities[self.spx].exchange.hours.get_next_trading_day(expiry)
        self.schedule.on(
            self.date_rules.on(next_trading_day),
            self.time_rules.after_market_open(self.spx, 1), 
            self.open_trades
        )
        
    def on_data(self, slice: Slice) -> None:
        # Scan every 5 minutes to check price convergence.
        if slice.time.minute % 5 == 0:
            exit_plan = self.copula_trader.exit_trades(self.time)
            # Exit the paired positions when the price converges.
            for contract, size in exit_plan.items():
                self.market_order(contract.symbol, size)
            
class CopulaTrader:
    copula = None
    copula_name = None
    security1_scaler = MinMaxScaler()
    security2_scaler = MinMaxScaler()
    traded_pairs = []
    
    def __init__(self, algorithm: QCAlgorithm, security1: Symbol, security2: Symbol, alpha: float = 0.05, misprice_threshold: float = 2.5) -> None:
        self._algorithm = algorithm
        # Interest rate and dividend yield providers to calculate fair option price later.
        self.interest_rate_provider = algorithm.risk_free_interest_rate_model
        self.security1_dividend_yield_provider = DividendYieldProvider(security1)
        self.security2_dividend_yield_provider = DividendYieldProvider(security2)
        # The significance level on KS test of the copula goodness-of-fit
        self.alpha = alpha
        # The threshold of the price divergence of a mispriced pair to have in order to start the positions.
        # Should at least over the transaction fee with some margin.
        self.misprice_threshold = misprice_threshold
        
    def fit_bivariate_copula(self, security1_prices: np.ndarray, security2_prices: np.ndarray) -> None:
        training_data = self._data_preparation(security1_prices, security2_prices)
        self._fit_bivariate_copula(training_data)
        
    def _data_preparation(self, security1_prices: np.ndarray, security2_prices: np.ndarray) -> np.ndarray:
        # Calculate log price difference for fitting copulas, since the series has more stationary domain for prediction.
        security1_log_price = np.log(security1_prices)
        security2_log_price = np.log(security2_prices)
        security1_log_diff = np.diff(security1_log_price)
        security2_log_diff = np.diff(security2_log_price)
        # Scale to [0, 1] to fit the model.
        scaled_security1_data = self.security1_scaler.fit_transform(security1_log_diff.reshape(-1, 1))
        scaled_security2_data = self.security2_scaler.fit_transform(security2_log_diff.reshape(-1, 1))
        data = np.column_stack((scaled_security1_data, scaled_security2_data))
        return data
        
    def _fit_bivariate_copula(self, data: np.ndarray) -> None:
        # Select the best-fitted bivariate copula by log-likelihood.
        self.copula = Bivariate.select_copula(data)
        self.copula_name = self.copula.copula_type
        
        # KS test to check if the actual data fits to the CDF of the copula good.
        samples = self.copula.sample(data.shape[0])
        p_value = self._ks2d2s(data[:, 0], samples[:, 0], data[:, 1], samples[:, 1])
        # Null hypothesis is the 2 datasets are having the same distribution, so if p < alpha, we reject the copula.
        if p_value < self.alpha:
            self.copula, self.copula_name = None, None
            self._algorithm.debug("No copula was fitted with statistically significant confidence.")
            return
        
        self._algorithm.debug(f"Best fitted copula distribution: {self.copula_name}, with tau: {self.copula.tau}")
        
    def _ks2d2s(self, x1: np.ndarray, y1: np.ndarray, x2: np.ndarray, y2: np.ndarray) -> float:
        '''Two-dimensional Kolmogorov-Smirnov test on two samples. 
        Adapted from: https://github.com/syrte/ndtest/blob/master/ndtest.py'''
        def avgmaxdist(x1, y1, x2, y2):
            D1 = maxdist(x1, y1, x2, y2)
            D2 = maxdist(x2, y2, x1, y1)
            return (D1 + D2) / 2
        
        def maxdist(x1, y1, x2, y2):
            n1 = len(x1)
            D1 = np.empty((n1, 4))
            for i in range(n1):
                a1, b1, c1, d1 = quadct(x1[i], y1[i], x1, y1)
                a2, b2, c2, d2 = quadct(x1[i], y1[i], x2, y2)
                D1[i] = [a1 - a2, b1 - b2, c1 - c2, d1 - d2]
            
            D1[:, 0] -= 1 / n1

            dmin, dmax = -D1.min(), D1.max() + 1 / n1
            return max(dmin, dmax)

        def quadct(x, y, xx, yy):
            n = len(xx)
            ix1, ix2 = xx <= x, yy <= y
            a = np.sum(ix1 & ix2) / n
            b = np.sum(ix1 & ~ix2) / n
            c = np.sum(~ix1 & ix2) / n
            d = 1 - a - b - c
            return a, b, c, d
        
        n1, n2 = len(x1), len(x2)
        D = avgmaxdist(x1, y1, x2, y2)

        sqen = np.sqrt(n1 * n2 / (n1 + n2))
        r1 = stats.pearsonr(x1, y1)[0]
        r2 = stats.pearsonr(x2, y2)[0]
        r = np.sqrt(1 - 0.5 * (r1**2 + r2**2))
        d = D * sqen / (1 + r * (0.25 - 0.75 / sqen))
        p = stats.kstwobign.sf(d)
        
        return p

    def scan_option_mispricing_combinations(self, security1_options: List[OptionContract], security2_options: List[OptionContract], current_security1_price: float, current_security2_price: float,
        current: datetime, n_samples: int = 1000) -> List[Tuple[OptionContract, OptionContract, float, float]]:
        # Get the simluated price series till the expiry. Note that you should use single expiry for all contracts for easier handling and stable theta.
        future_prices, dtm = self._get_simulated_paths(current_security1_price, current_security2_price, security1_options[0].expiry, current, n_samples)
        
        mispriced_pairs = []
        interest_rate = self.interest_rate_provider.get_interest_rate(current)
        security1_dividend_yield = self.security1_dividend_yield_provider.get_dividend_yield(current)
        security2_dividend_yield = self.security2_dividend_yield_provider.get_dividend_yield(current)

        # Separate call and put options to avoid mixed right pairs, in order to keep theta close to 0.
        for right in [OptionRight.CALL, OptionRight.PUT]:
            sorted_security1_options = sorted([contract for contract in security1_options if contract.right == right], key=lambda x: x.strike)
            sorted_security2_options = sorted([contract for contract in security2_options if contract.right == right], key=lambda x: x.strike)
            ttm = dtm / 365

            # Calculate the security1-security2 fair prices and spot any significant mispricing.
            for i, security1_option in enumerate(sorted_security1_options):
                for j, security2_option in enumerate(sorted_security2_options):
                    # Skip the pairs already being traded.
                    if (security1_option.symbol, security2_option.symbol) in [(y.symbol for y in x[0]) for x in self.traded_pairs]:
                        continue
                    
                    # Calculate the probability of price converges. Since the ATM options are the most efficiently priced, we use that as a proxy for our win rate.
                    # The probability will be based on the whether the simulated paths have ever reached the point (so it was ever ATM).
                    prob = self._ratio_reached(self.paths, [security1_option.strike, security2_option.strike])

                    security1_price = self._calculate_fair_option_price(future_prices, ttm, security1_option.strike, right, interest_rate, security1_dividend_yield, False)
                    security2_price = self._calculate_fair_option_price(future_prices, ttm, security2_option.strike, right, interest_rate, security2_dividend_yield, True)
                    # Add to trade stacks only if the mispricing is opposite in direction and above profit threshold.
                    security1_price_divergence = security1_price - security1_option.ask_price
                    security2_price_divergence = security2_price - security2_option.bid_price
                    price_divergence1 = security1_price_divergence - security2_price_divergence
                    price_divergence2 = security1_price - security1_option.bid_price - security2_price + security2_option.ask_price
                    price_divergence = price_divergence1 if abs(price_divergence1) > abs(price_divergence2) else price_divergence1
                    if abs(price_divergence) > self.misprice_threshold and np.sign(security1_price_divergence) != np.sign(security2_price_divergence):
                        mispriced_pairs.append((security1_option, security2_option, price_divergence, prob))
        
        self._algorithm.debug(f"Found {len(mispriced_pairs)} mispriced option contract pairs.")

        return mispriced_pairs
    
    def _get_simulated_paths(self, current_security1_price: float, current_security2_price: float, expiry: datetime, current: datetime, n_samples: int) -> Tuple[float, float]:
        # Get the year till expiry.
        dtm = (expiry - current).total_seconds() / 60 / 60 / 24
        
        future_log_prices = np.log(np.array([[[current_security1_price, current_security2_price]] * n_samples]))
        # Convert to estimated trading days left.
        for _ in range(int(dtm / 252 * 365)):
            # The future price is simulated from N stochastic simulations.
            future_log_diff = self.copula.sample(n_samples)
            # Convert the daily log-difference into future price.
            security1_log_diff = self.security1_scaler.inverse_transform(future_log_diff[:, 0].reshape(-1, 1))
            security2_log_diff = self.security2_scaler.inverse_transform(future_log_diff[:, 1].reshape(-1, 1))
            log_diff = np.column_stack((security1_log_diff, security2_log_diff))
            future_log_prices = np.concatenate([future_log_prices, np.array([future_log_prices[-1, :, :] + log_diff])], axis=0)
        
        self.paths = np.exp(future_log_prices)
        # Return the ultimate price at the last iteration, convert back to price from log-price.
        return self.paths[-1], dtm

    def _calculate_fair_option_price(self, future_prices: np.ndarray, ttm: float, strike: float, right: OptionRight, interest_rate: float, dividend_yield: float, security2: bool = False) -> float:
        select_col = 1 if security2 else 0
        future_prices = future_prices[:, select_col]
        
        # Average of option payoffs among simulation paths. Make use of vectorize calculation here instead of util method.
        option_prices = np.maximum(future_prices - strike, 0) if right == OptionRight.CALL else np.maximum(strike - future_prices, 0)
        # Adjust the continuous dividend payoff yield and interest rate.
        return np.exp((dividend_yield - interest_rate) * ttm) * np.mean(option_prices)
    
    def _ratio_reached(self, data: np.ndarray, point: np.ndarray) -> float:
        # Count how many paths ever reached the point.
        count = 0
        for i in range(data.shape[1]):
            if point[0] <= max(data[:, i, 0]) and point[1] <= max(data[:, i, 1]) and point[0] >= min(data[:, i, 0]) and point[1] >= min(data[:, i, 1]):
                count += 1
        # Calculate the ratio of paths that the point has ever been reached.
        return count / data.shape[1]

    def trade_options(self, mispriced_pairs: List[Tuple[OptionContract, OptionContract, float, float]], fund: float, contract_multiplier: int = 100) -> Dict[OptionContract, int]:
        orders = {}
        total_pct = 0

        # Only trade on the top 10 expected return pairs.
        top_expected_ret = sorted(mispriced_pairs, key=lambda x: abs(x[2]) * x[3], reverse=True)[:10]
        for security1_option, security2_option, price_divergence, prob in top_expected_ret:
            # Calculate the order size of the mispricing pairs.
            contract1_price = security1_option.ask_price if price_divergence > 0 else security1_option.bid_price
            contract2_price = security2_option.ask_price if price_divergence < 0 else security2_option.bid_price
            security1_option_order_size, security2_option_order_size, order_pct = self._calculate_order_size(price_divergence, fund, prob, contract1_price, contract2_price, contract_multiplier)
            # Only order those with positive Kelly sizing and keep the exposure to cash only.
            # Keep 5% buffer to avoid order errors.
            if order_pct and total_pct + order_pct <= 0.95:
                if security1_option not in orders:
                    orders[security1_option] = 0
                if security2_option not in orders:
                    orders[security2_option] = 0
            # Aggregate the overall order sizes between all pairs.
                orders[security1_option] += security1_option_order_size
                orders[security2_option] += security2_option_order_size
                total_pct += order_pct
                self.traded_pairs.append(((security1_option, security2_option), (security1_option_order_size, security2_option_order_size)))

        return orders
            
    def _calculate_order_size(self, price_divergence: float, fund: float, prob_win: float, security1_option_price: float, security2_option_price: float, contract_multiplier: int) -> Tuple[int, int, float]:
        # The profit percentage is based on the option prices.
        capital = security1_option_price + security2_option_price
        profit_pct = abs(price_divergence) / capital
        # Assume no recovery at expiry if the price does not converges, while no extra loss will be paid.
        # To improve, you may use a continuous distribution to model the aggregated profit.
        # Keep at most 5% per trade, since option has leverage effect.
        order_pct = min(prob_win - (1 - prob_win) / profit_pct, 0.05)
        # The order size should be the shared by both side of the legs.
        order_size = order_pct * fund / capital // contract_multiplier
        order_pct = order_size * capital / fund
        # If the optimal order size is negative, do not place order.
        if order_pct < 0:
            return 0, 0, 0
        # If price divergence above 0, meaning security1 option is underpriced and the security2 option is overpriced, so we buy the security1 option and sell the security2 option.
        if price_divergence > 0:
            return order_size, -order_size, order_pct
        # Vice versa otherwise.
        return -order_size, order_size, order_pct

    def exit_trades(self, current: datetime) -> Dict[OptionContract, int]:
        # Get the parameters for fair price calculation.
        interest_rate = self.interest_rate_provider.get_interest_rate(current)
        security1_dividend_yield = self.security1_dividend_yield_provider.get_dividend_yield(current)
        security2_dividend_yield = self.security2_dividend_yield_provider.get_dividend_yield(current)

        exit_positions = {}
        for ((contract1, contract2), (size1, size2)) in self.traded_pairs.copy():
            # Get the simluated price series till the expiry.
            future_prices = self.paths[-1]
            ttm = (contract1.expiry - current).total_seconds() / 60 / 60 / 24 / 365
            # Check if the price discrepancy converges (relatively).
            contract1_price = self._calculate_fair_option_price(future_prices, ttm, contract1.strike, contract1.right, interest_rate, security1_dividend_yield, False)
            contract2_price = self._calculate_fair_option_price(future_prices, ttm, contract2.strike, contract2.right, interest_rate, security2_dividend_yield, True)
            contract1.mid_price = (contract1.bid_price + contract1.ask_price) * 0.5
            contract2.mid_price = (contract2.bid_price + contract2.ask_price) * 0.5
            contract1_divergence = contract1_price - contract1.mid_price
            contract2_divergence = contract2_price - contract2.mid_price
            price_divergence = contract1_divergence - contract2_divergence
            
            # If so, place the opposite size to exit the positions.
            if (size1 > 0 and price_divergence <= 0) or (size1 < 0 and price_divergence >= 0):
                if contract1 not in exit_positions:
                    exit_positions[contract1] = 0
                if contract2 not in exit_positions:
                    exit_positions[contract2] = 0
                exit_positions[contract1] -= size1
                exit_positions[contract2] -= size2
                # Remove the record and allow the pair to be traded again.
                self.traded_pairs.remove(((contract1, contract2), (size1, size2)))

        return exit_positions