In This Page

Introduction

Implementation

Strategy Payoff

Example

Option Strategies

Long Jelly Roll

Introduction

A long Jelly Roll, or simply Roll, is a combination of a long call calendar spread and a short put calendar spread. It consists of buying a put and selling a call of the same expiry, as well as buying a call and selling a put with a further expiry, where all of the contracts have the same strike price. This strategy serves as an arbitrage on Option mispricing due to the temporary disparity between the call spread and the put spread synthetic portfolios. It is a delta-, gamma-, vega-, and theta-neutral strategy, but sensitive to rho (interest rate) and phi (dividend yield).

Implementation

Follow these steps to implement the long jelly roll strategy:

In the Initializeinitialize method, set the start date, set the end date, and create an Option universe.

Select Language:

private Symbol _symbol;

public override void Initialize()
{
    SetStartDate(2017, 4, 1);
    SetEndDate(2017, 4, 22);
    SetCash(100000);

    UniverseSettings.Asynchronous = true;
    var option = AddOption("GOOG", Resolution.Minute);
    _symbol = option.Symbol;
    option.SetFilter(x => x.IncludeWeeklys().JellyRoll(5m, 30, 60));
}

def initialize(self) -> None:
    self.set_start_date(2017, 4, 1)
    self.set_end_date(2017, 4, 22)
    self.set_cash(100000)

    self.universe_settings.asynchronous = True
    option = self.add_option("GOOG", Resolution.MINUTE)
    self._symbol = option.symbol
    option.set_filter(lambda x: x.include_weeklys().jelly_roll(5.0, 30, 60))

In the OnDataon_data method, select the expiry and strikes of the contracts in the strategy legs.

Select Language:

public override void OnData(Slice slice)
{
    if (Portfolio.Invested) return;

    // Get the OptionChain
    if (!slice.OptionChains.TryGetValue(_symbol, out var chain))
    {
        return;
    }

    // Select expiry dates and strike price
    var strike = chain.OrderBy(x => Math.Abs(chain.Underlying.Price - x.Strike)).First().Strike;
    var contracts = chain.Where(x => x.Strike == strike).ToList();
    var farExpiry = contracts.Max(x => x.Expiry);
    var nearExpiry = contracts.Min(x => x.Expiry);

def on_data(self, slice: Slice) -> None:
    if self.portfolio.invested:
        return

    # Get the OptionChain
    chain = slice.option_chains.get(self._symbol, None)
    if not chain:
        return

    # Select an expiry date and ITM & OTM strike prices
    strike = sorted([x.strike for x in chain], key=lambda x: abs(x - chain.underlying.price))[0]
    contracts = [x for x in chain if x.strike == strike]
    far_expiry = max([x.expiry for x in contracts])
    near_expiry = min([x.expiry for x in contracts])

In the OnDataon_data method, select the contracts and place the order.

Approach A: Call the OptionStrategies.JellyRollOptionStrategies.jelly_roll method with the details of each leg and then pass the result to the Buybuy method.

Select Language:

var jellyRoll = OptionStrategies.JellyRoll(_symbol, strike, nearExpiry, farExpiry);
Buy(jellyRoll, 1);

jelly_roll = OptionStrategies.jelly_roll(self._symbol, strike, near_expiry, far_expiry)
self.buy(jelly_roll, 1)

Approach B: Create a list of Leg objects and then call the Combo Market Ordercombo_market_order, Combo Limit Ordercombo_limit_order, or Combo Leg Limit Ordercombo_leg_limit_order method.

Select Language:

// Select the call and put contracts
var nearCall = contracts.Single(x => x.Expiry == nearExpiry && x.Right == OptionRight.Call);
var farCall = contracts.Single(x => x.Expiry == farExpiry && x.Right == OptionRight.Call);
var nearPut = contracts.Single(x => x.Expiry == nearExpiry && x.Right == OptionRight.Put);
var farPut = contracts.Single(x => x.Expiry == farExpiry && x.Right == OptionRight.Put);

var legs = new List<Leg>()
{
    Leg.Create(nearCall.Symbol, -1),
    Leg.Create(farCall.Symbol, 1),
    Leg.Create(nearPut.Symbol, 1),
    Leg.Create(farPut.Symbol, -1),
};
ComboMarketOrder(legs, 1);

# Select the call and put contracts
near_call = next(filter(lambda x: x.right == OptionRight.CALL and x.expiry == near_expiry, contracts))
far_call = next(filter(lambda x: x.right == OptionRight.CALL and x.expiry == far_expiry, contracts))
near_put = next(filter(lambda x: x.right == OptionRight.PUT and x.expiry == near_expiry, contracts))
call_put = next(filter(lambda x: x.right == OptionRight.PUT and x.expiry == far_expiry, contracts))           

legs = [
    Leg.create(near_call.symbol, -1),
    Leg.create(far_call.symbol, 1),
    Leg.create(near_put.symbol, 1),
    Leg.create(call_put.symbol, -1),
]
self.combo_market_order(legs, 1)

Strategy Payoff

This is a delta-, gamma-, vega-, and theta-neutral strategy. The payoff is

$\begin{array}{rcll} C_{T_1}^{T_1} & = & (S_{T_1} - K)^{+}\\ P_{T_1}^{T_1} & = & (K - S_{T_1})^{+}\\ Payoff_{T_1} & = & (P_{T_1}^{T_1} - P_{T_0}^{T_1} - C_{T_1}^{T_1} + C_{T_0}^{T_1} + C_{T_1}^{T_2} - C_{T_0}^{T_2} - P_{T_1}^{T_2} + P_{T_0}^{T_2})\times m - fee\\ \end{array}$

$\begin{array}{rcll} \textrm{where} & C_{T_1}^{T_1} & = & \textrm{Market value of Call with expiry at T1 at time T1}\\ & C_{T_1}^{T_2} & = & \textrm{Market value of Call with expiry at T2 at time T1}\\ & P_{T_1}^{T_1} & = & \textrm{Market value of Put with expiry at T1 at time T1}\\ & P_{T_1}^{T_2} & = & \textrm{Market value of Put with expiry at T2 at time T1}\\ & S_{T_1} & = & \textrm{Underlying asset price at time T1}\\ & K & = & \textrm{Strike price}\\ & Payoff_T & = & \textrm{Payout total at time T}\\ & C_{T_0}^{T_1} & = & \textrm{Market value of Call with expiry at T1 when the trade opened}\\ & C_{T_0}^{T_2} & = & \textrm{Market value of Call with expiry at T2 when the trade opened}\\ & P_{T_0}^{T_1} & = & \textrm{Market value of Put with expiry at T2 when the trade opened}\\ & P_{T_0}^{T_2} & = & \textrm{Market value of Put with expiry at T2 when the trade opened}\\ & m & = & \textrm{Contract multiplier}\\ & T_1 & = & \textrm{Time T1 as the near expiration}\\ & T_2 & = & \textrm{Time T2 as the far expiration} \end{array}$

The following chart shows the payoff at expiration:

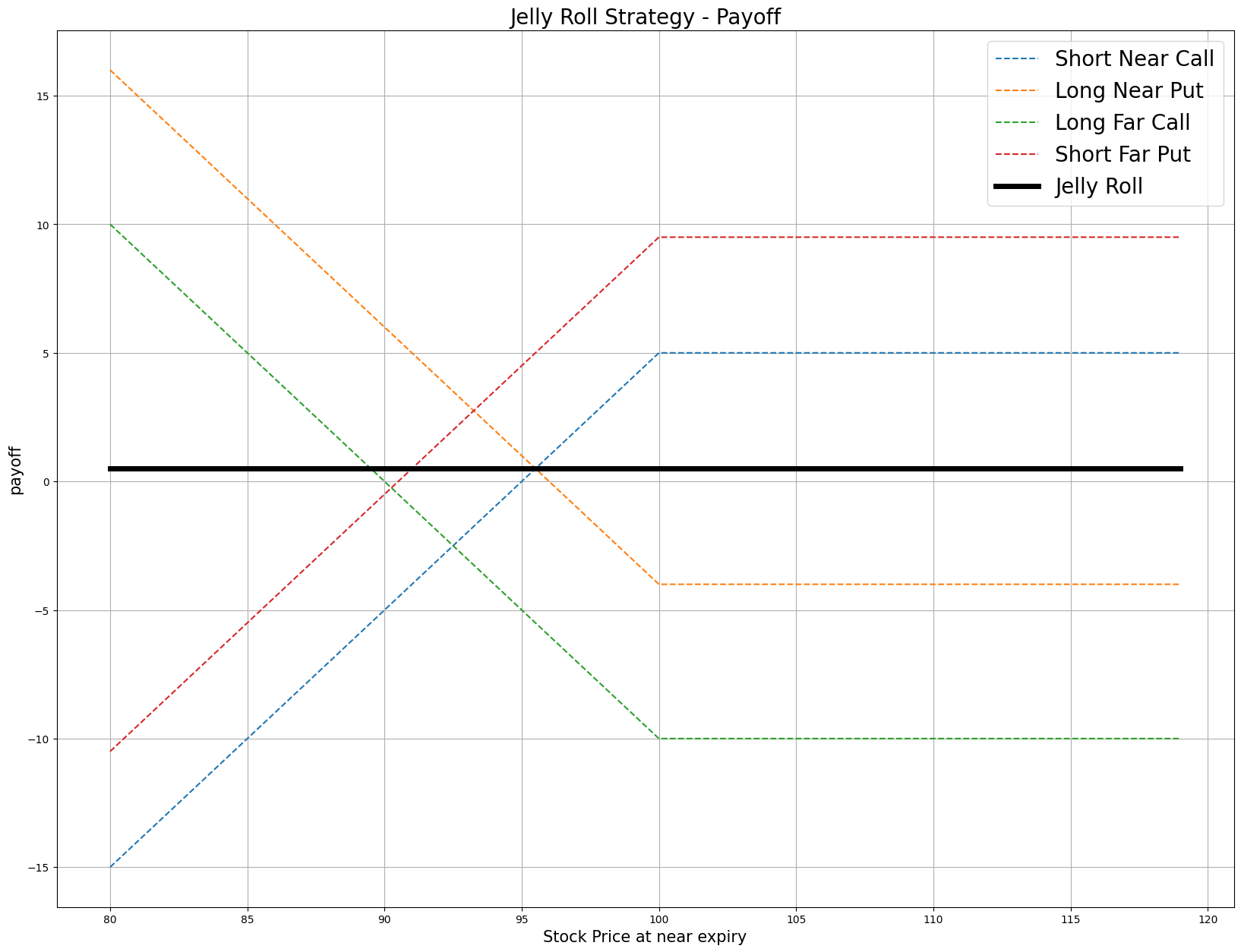
The payoff is dependent on the market prices of the Options, but in theory, if assuming call-put parity exists, the expected payoff would be

$\begin{array}{rcll} Payoff_{T_1} & = & Payoff_{\textrm{call calendar spread}} - Payoff_{\textrm{put calendar spread}}\\ & = & K \times (T_2 - T_1) \times r - D \end{array}$

$\begin{array}{rcll} \textrm{where} & r & = & \textrm{Continuous compounding interest rate}\\ & D & = & \textrm{Dividend payment during the life of the option} \end{array}$

If the Option is American Option, there is a risk of early assignment on the contracts you sell.

Example

The following table shows the price details of the assets in the algorithm:

Asset	Price at position open ($)	Price at the first expiry ($)	Strike ($)
Near-expiry Call	18.50	23.75	832.50
Near-expiry Put	22.50	12.85	832.50
Far-expiry Call	23.90	24.45	832.50
Far-expiry Put	19.00	13.70	832.50
Underlying Equity	-	843.2500	-

Therefore, the payoff is

$\begin{array}{rcll} Payoff_{T_1} & = & (P_{T_1}^{T_1} - P_0^{T_1} - C_{T_1}^{T_1} + C_0^{T_1} + C_{T_1}^{T_2} - C_0^{T_2} - P_{T_1}^{T_2} + P_0^{T_2})\times m - fee\\ & = & (12.85 - 22.50 - 23.75 + 18.50 + 24.45 - 23.90 - 13.70 + 19.00)\times100 - 1.00\times4\\ & = & -909.00\\ \end{array}$

So, the strategy loses $909.

The following algorithm implements a long jelly roll Option strategy:

Select Language:

public class JellyRollStrategy : QCAlgorithm
{
    private Symbol _symbol;

    public override void Initialize()
    {
        SetStartDate(2017, 4, 1);
        SetEndDate(2017, 4, 23);
        SetCash(100000);

        var option = AddOption("GOOG", Resolution.Minute);
        _symbol = option.Symbol;
        option.SetFilter(universe => universe.IncludeWeeklys().JellyRoll(5m, 30, 60));
    }

    public override void OnData(Slice slice)
    {
        if (Portfolio.Invested ||
            !slice.OptionChains.TryGetValue(_symbol, out var chain))
        {
            return;
        }

        // Select expiry dates and strike price
        var strike = chain.OrderBy(x => Math.Abs(chain.Underlying.Price - x.Strike)).First().Strike;
        var contracts = chain.Where(x => x.Strike == strike).ToList();
        var farExpiry = contracts.Max(x => x.Expiry);
        var nearExpiry = contracts.Min(x => x.Expiry);

        // Order Strategy
        var jellyRoll = OptionStrategies.JellyRoll(_symbol, strike, nearExpiry, farExpiry);
        Buy(jellyRoll, 1);
    }
}

class JellyRollOptionStrategy(QCAlgorithm):
    def initialize(self) -> None:
        self.set_start_date(2017, 4, 1)
        self.set_end_date(2017, 4, 23)
        self.set_cash(100000)
        
        option = self.add_option("GOOG", Resolution.MINUTE)
        self._symbol = option.symbol

        # set our strike/expiry filter for this option chain
        option.set_filter(lambda x: x.include_weeklys().jelly_roll(5.0, 30, 60))

    def on_data(self, slice: Slice) -> None:
        if self.portfolio.invested:
            return

        # Get the OptionChain
        chain = slice.option_chains.get(self._symbol, None)
        if not chain:
            return

        # Select an expiry date and ITM & OTM strike prices
        strike = sorted([x.strike for x in chain], key=lambda x: abs(x - chain.underlying.price))[0]
        contracts = [x for x in chain if x.strike == strike]
        far_expiry = max([x.expiry for x in contracts])
        near_expiry = min([x.expiry for x in contracts])

        jelly_roll = OptionStrategies.jelly_roll(self._symbol, strike, near_expiry, far_expiry)
        self.buy(jelly_roll, 1)

You can also see our Videos. You can also get in touch with us via Discord.

Did you find this page helpful?

Contribute to the documentation:

Browse

Cloud Platform

Writing Algorithms

▶
Key Concepts

Initialization

▶
Securities

▶
Portfolio

▶
Universes

▶
Datasets

▶
Importing Data

▶
Consolidating Data

▶
Historical Data

▶
Trading and Orders

▶
Reality Modeling

Scheduled Events

▶
Indicators

Object Store

▶
Optimization

▶
Machine Learning

▶
Algorithm Framework

Charting

Logging

▶
Statistics

▶
Live Trading

Strategy Library

API Reference

▶
Migrations

Research Environment

Local Platform

LEAN CLI

LEAN Engine

Hello

Option Strategies

Long Jelly Roll

Introduction

Implementation

Strategy Payoff

Example

SIGN IN

Browse

Cloud Platform

Writing Algorithms

▶Key Concepts

Initialization

▶Securities

▶Portfolio

▶Universes

▶Datasets

▶Importing Data

▶Consolidating Data

▶Historical Data

▶Trading and Orders

▶Reality Modeling

Scheduled Events

▶Indicators

Object Store

▶Optimization

▶Machine Learning

▶Algorithm Framework

Charting

Logging

▶Statistics

▶Live Trading

Strategy Library

API Reference

▶Migrations

Research Environment

Local Platform

LEAN CLI

LEAN Engine

Hello

Option Strategies

Long Jelly Roll

Introduction

Implementation

Strategy Payoff

Example

▶
Key Concepts

▶
Securities

▶
Portfolio

▶
Universes

▶
Datasets

▶
Importing Data

▶
Consolidating Data

▶
Historical Data

▶
Trading and Orders

▶
Reality Modeling

▶
Indicators

▶
Optimization

▶
Machine Learning

▶
Algorithm Framework

▶
Statistics

▶
Live Trading

▶
Migrations