Introduction
In this research post, we examine a strategy that concentrates the portfolio on assets with low beta. To diversify the portfolio and avoid making large bets on any single industry, the algorithm gives equal weight to each industry group. The results show that the strategy outperforms buy-and-hold but still exhibits a beta of 0.79. The algorithm we implement in this post is inspired by the research of Asness, Frazzini, and Pedersen (2013).
Background
Beta is a decimal number that describes the scale and direction of an asset’s returns relative to movements in the underlying benchmark. A beta of 1 means that the asset moves perfectly in tandem with the underlying benchmark. That is, when the benchmark moves up in price, the asset makes the same move in price. A beta above 1 means the asset moves in the same direction as the underlying benchmark, but moves further in that direction. A beta of -1 means the asset moves in the opposite direction as the underlying benchmark. Lastly, a beta of 0 means the asset’s returns aren’t influenced by movements in the underlying benchmark.
To calculate beta, we can use linear regression with the benchmark’s daily return as the independent variable and the asset’s daily return as the dependent variable.
where
- is the slope of the regression line,
- is the number of observations,
- and are individual data points for the independent and dependent variables, respectively,
- is the mean of the independent variable (the benchmark’s daily return),
- is the mean of the dependent variable (the asset’s daily return)
There are several ways to construct a low-beta portfolio. In this research, we use the US Fundamental dataset from Morningstar to group the stocks by their respective industry group. Then, we select the most liquid stocks from each group. We calculate the absolute beta values for all the selected stocks over the trailing trading days and narrow the universe down to just the stocks below the median beta value.
To determine the position size of each asset, we weight the assets of each group by their beta value so that assets with a lower absolute beta value are given a greater allocation in the portfolio. To avoid making a large bet on any single industry group, we give an equal allocation to each industry group.
Implementation
To implement this strategy, we start by adding the underlying benchmark in the initialize method.
self._spy = self.add_equity('SPY', Resolution.DAILY)
Next, we add a universe that selects assets at the start of each month.
self.universe_settings.resolution = Resolution.DAILYself.universe_settings.schedule.on(self.date_rules.month_start(self._spy.symbol))self.add_universe(self._select_assets)
To end the initialize method, we add a Scheduled Event to rebalance the portfolio each month.
self.schedule.on(self.date_rules.month_start(self._spy.symbol, 2), self.time_rules.midnight, self._rebalance)
In the _select_assets function, we start by selecting the most liquid assets of each industry group.
fundamentals = sorted([f for f in fundamentals if f.asset_classification.morningstar_industry_group_code], key=lambda f: (f.asset_classification.morningstar_industry_group_code, f.dollar_volume))selected = []for _, industry_group_fundamentals in itertools.groupby(fundamentals, lambda f: f.asset_classification.morningstar_industry_group_code):selected.extend(list(industry_group_fundamentals)[-self._assets_per_industry:])
We then calculate the absolute beta of each asset and the median value.
self._beta_by_symbol = self._beta([f.symbol for f in selected]).abs()median_beta = np.median(self._beta_by_symbol.values)
Next, we select the assets in each industry that have an absolute beta below the median value and calculate their portfolio weights. We take the absolute value of beta because we want to allocate to assets that aren't impacted by movements in the underlying benchmark. Two assets with a beta of 1 and -1 move in opposite directions, but they are both impacted by movements in the underlying benchmark. We used the median beta as the threshold value to ensure the portfolio is diversified across many assets. If we use an arbitrary number, it may lead to a small universe, and it introduces a parameter that can cause the algorithm to be overfit.
weights_by_industry = {}symbols = []for industry_code, industry_assets in itertools.groupby(selected, lambda f: f.asset_classification.morningstar_industry_group_code):industry_beta_by_symbol = self._beta_by_symbol[[f.symbol for f in industry_assets if f.symbol in self._beta_by_symbol]]low_betas = industry_beta_by_symbol[industry_beta_by_symbol < median_beta]if low_betas.empty:continuesymbols.extend(list(low_betas.index))beta_ranks = low_betas.sort_values().rank(method='first', ascending=False)weights_by_industry[industry_code] = beta_ranks / beta_ranks.sum()
To end the _select_assets function, we scale the weights so that each industry is given an equal allocation in the portfolio, create the final portfolio targets, and then return the selected assets to define the universe. These portfolio targets define the weight of each asset in the target portfolio. We use this approach instead of manually calling the method for two reasons. First, this logic is in the universe selection function, so the assets aren't in the universe yet. Second, when we use PortfolioTarget objects, LEAN intelligently sorts the orders based on our position delta and then places the orders that reduce our position size in an asset before it places orders that increase our position size in an asset.
self._targets = [PortfolioTarget(symbol, 0) for symbol, holding in self.portfolio.items() if holding.invested and symbol not in symbols]for industry_assets in weights_by_industry.values():self._targets.extend([PortfolioTarget(symbol, weight/len(weights_by_industry)) for symbol, weight in industry_assets.items()])return symbols
To efficiently calculate the beta of all the assets during universe selection, we define a _beta function, adapted from this Stack Overflow thread. This code structure is beneficial because you can explore almost any feature by simply replacing this _beta function.
def _beta(self, symbols):returns = self.history([self._spy.symbol] + symbols, self._beta_period, Resolution.DAILY, fill_forward=False).close.unstack(0).dropna(axis=1).pct_change().dropna()symbols = [s for s in symbols if s in returns.columns]df = returns[[self._spy.symbol] + symbols]X = df.values[:, [0]] # first column is the marketX = np.concatenate([np.ones_like(X), X], axis=1) # prepend a column of ones for the interceptb = np.linalg.pinv(X.T.dot(X)).dot(X.T).dot(df.values[:, 1:]) # matrix algebrareturn pd.Series(b[1], df.columns[1:], name='Beta')
In the _rebalance function that runs once per month, we use the portfolio targets we created earlier to rebalance the portfolio.
def _rebalance(self):if self._targets:self.set_holdings(self._targets)self._targets = []
Results
We backtested the algorithm from January 2010 to the current day. The benchmark is buy-and-hold with the SPY, which produced a 0.624 Sharpe ratio. In contrast, the low beta portfolio strategy generated a 0.669 Sharpe ratio. Therefore, the strategy outperformed buy-and-hold.
To test the sensitivity of the parameters chosen, we ran a parameter optimization job. We tested a beta lookback period of 10 days to 60 days in steps of 25 days and we tested the number of assets per industry group between 10 and 100 in steps of 10. Of the 30 parameter combinations, 19 (63.3%) produced a greater Sharpe ratio than the benchmark. The following image shows the heatmap of Sharpe ratios for the parameter combinations:
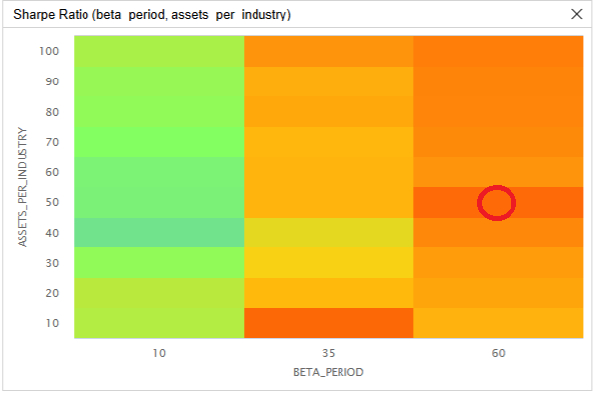
The red circle in the preceding image identifies the parameters we chose as the strategy's default. We chose an beta period of 60 and 50 assets per industry group because it was in the center of an area of least sensitive parameter combinations.
Even though the strategy targets assets with low beta, the results show the backtest produced a beta of 0.79. We conclude this is because most assets have a strong relationship to the underlying benchmark. Therefore, even though we select assets with an absolute beta value below the universe median, many of the selected assets may still have a beta closer to 1 than 0. Furthermore, beta estimates are backward-looking and volatile, so an asset that displays a low beta over some lookback period may have a high beta over the following month.
We estimate that the industry groups within the technology sector have the beta values closest to 1 because the technology sector has the largest representation in the S&P 500 Index, which is our underlying benchmark. Further exploration can be done by excluding assets from the universe that fall within the technology sector.
References
- Asness, Cliff S. and Frazzini, Andrea and Pedersen, Lasse Heje, Low-Risk Investing Without Industry Bets (May 10, 2013). Available at SSRN: https://ssrn.com/abstract=2259244 or http://dx.doi.org/10.2139/ssrn.2259244




















Decebal Mihailescu
Be aware the large number of trades that generates a lot of fees when rebalancing.
If your portfolio is less than $25K you will lose money long term.
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
To unlock posting to the community forums please complete at least 30% of Boot Camp.
You can continue your Boot Camp training progress from the terminal. We hope to see you in the community soon!