Introduction
In this research post, we review the Kelly criterion and apply it to scale trade sizes. This mathematical formula determines the ideal sizes while balancing the objectives of maximizing long-term capital accumulation and avoiding the risk of ruin. The algorithm we implement in this post is a simple signal with intelligent risk control that you can adapt to a wide range of trading strategies.
Background
In the application of bet sizing, the Kelly criterion represents how much to bet each trade in order to maximize your long-term growth rate. This type of scaling is appropriate for a strategy that attempts to time entry and exit points on an individual asset. The calculation for sizing the bet of a single entry is
Bet size=Pr(profit)−Pr(loss)win/loss ratio=Pr(profit)−1−Pr(profit)win/loss ratio
In a trading strategy, we don’t know the true values of these inputs, but we can estimate them from the trailing performance of the strategy. The calculations can lead to an exposure less than 100%. In these cases, you can allocate the remaining exposure to a risk-free asset to avoid holding cash.
Implementation
To implement a strategy that scales trades based on the Kelly criterion, we start by adding a risky and risk-free asset in the initialize method.
self._risk_asset = self.add_equity('IBM', Resolution.HOUR, leverage=6)self._rf_asset = self.add_equity('SHY', Resolution.HOUR, leverage=6)
You can apply this bet sizing logic to any type of strategy. In this example, we’ll apply it to a simple moving average (SMA) crossover strategy, so let’s add the indicators.
self._risk_asset.short_sma = self.sma(self._risk_asset.symbol, 1)self._risk_asset.long_sma = self.sma(self._risk_asset.symbol, 6)
Next, we define a variable to track the strategy signal (1=in; 0=out) and create an instance of the KellyCriterion class, which we’ll define later. The first argument (1.5) you pass to the constructor defines the scaling factor to apply to the Kelly criterion. For example, 2 is double Kelly and 0.5 is half Kelly. The second argument (40) you pass to the constructor defines the number of historical trades to use when calculating the probability of profit and the win-loss ratio of the strategy.
self._risk_asset.signal = 0self._kelly_criterion = KellyCriterion(1.5, 40)
To end the initialize method, add a warm-up period so that you have some historical performance of the strategy before you start placing trades.
self.set_warm_up(timedelta(365))
In the on_data method, we first instruct the algorithm to wait until the market is open to avoid trading errors.
if not data.bars or not self.is_market_open(self._risk_asset.symbol):return
Next, we check if we need to update the strategy signal and then use the new signal to update the KellyCriterion object.
if not self._risk_asset.signal and self._risk_asset.short_sma > self._risk_asset.long_sma:self._risk_asset.signal = 1self._kelly_criterion.update_signal(1, self._risk_asset.price)elif self._risk_asset.signal and self._risk_asset.short_sma < self._risk_asset.long_sma:self._risk_asset.signal = 0self._kelly_criterion.update_signal(0, self._risk_asset.price)
If the algorithm is still warming-up or the we don’t have enough trade samples yet for the KellyCriterion object, we just do nothing for this time step.
if self.is_warming_up or not self._kelly_criterion.is_ready:return
Otherwise, we update the portfolio holdings based on the signal. If the strategy signals we should enter, we buy the risky asset while capping the exposure to 575% to avoid errors. If the strategy signals we should exit, we allocate 100% of the portfolio to the risk-free asset.
if self._risk_asset.signal and not self._risk_asset.holdings.is_long:weight = min(5.75, self._kelly_criterion.weight())self.set_holdings([PortfolioTarget(self._risk_asset.symbol, weight),PortfolioTarget(self._rf_asset.symbol, 0 if weight > 1 else 1-weight)])elif not self._risk_asset.signal and self._risk_asset.holdings.is_long:self.set_holdings([PortfolioTarget(self._rf_asset.symbol, 1)], True)
In the __init__ method of the KellyCriterion class, we save the lookback period and create a list to store the historical trade results.
def __init__(self, factor, period):self._factor = factorself._period = periodself._trades = np.array([])
In the update_signal method, we record the purchase price at each entry and save the trade result at each exit. This implementation is effectively assuming a fixed trade size of 1 so that the resulting bet size isn't affected by previous bet sizes we calculate.
def update_signal(self, signal, price):if signal: # Enterself._entry_price = priceelse: # Exitself._trades = np.append(self._trades, [price - self._entry_price])[-self._period:]
In the weight method, we calculate the trade size using the formula above.
def weight(self):if not self.is_ready:return Nonewins = self._trades[self._trades > 0]losses = self._trades[self._trades < 0]if not losses.sum():return self._factorif not wins.sum():return 0win_loss_ratio = wins.mean() / losses.mean()winning_probability = len(wins) / self._periodreturn self._factor*(winning_probability - (1-winning_probability)/win_loss_ratio)
The is_ready property checks if there are enough trade samples to calculate the trade size.
@propertydef is_ready(self):return len(self._trades) == self._period
Results
We can measure the performance of some discrete bet sizing strategies with absolute return instead of their relative return to the SPY because in some cases it may not make sense to judge their performance against the SPY. Furthermore, we should excluded trading fees to focus the research on the portfolio weighting, not the signal.
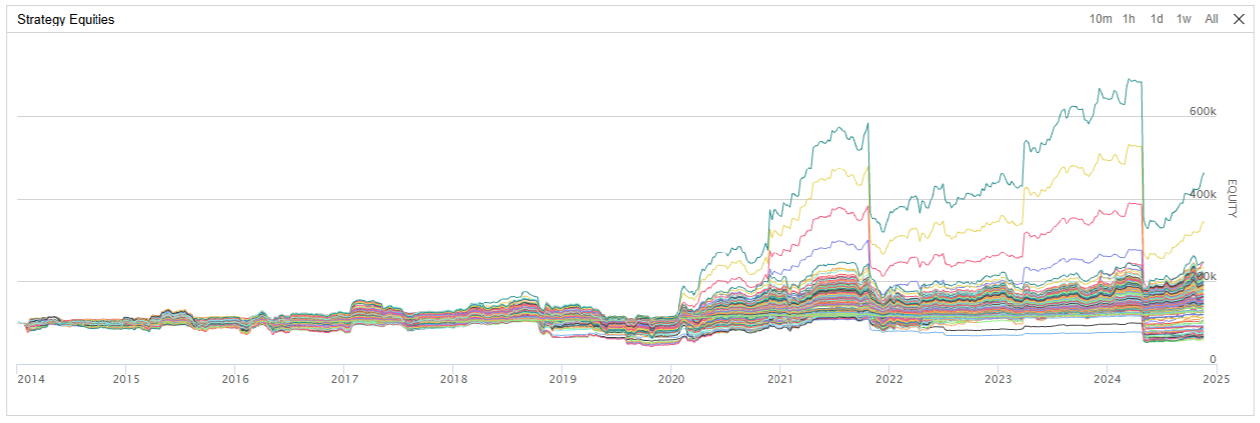
We backtested the algorithm from January 2014 to the current day to get about 10 years of historical performance. The benchmark we chose was an SMA crossover with a weight of either 0 or 1 for each asset, which produced the following metrics:
- Return: 74%
- Drawdown: 24%
- Sharpe ratio: 0.183
- Average daily IBM weight: 47.3%
In contrast, after integrating the Kelly criterion bet sizing logic, the strategy produced the following metrics:
- Return: 109%
- Drawdown: 24%
- Sharpe ratio: 0.262
- Average daily IBM weight: 51.8%
Therefore, by integrating the Kelly criterion bet sizing, the strategy outperforms the benchmark in terms of return, which is the goal of the Kelly criterion. Another goal of the Kelly criterion is to reduce drawdowns when the strategy signal leads to losses. In this case, the benchmark algorithm demonstrates the strategy is profitable, so the Kelly criterion increases the return while maintaining the drawdown, ultimately leading to an increase in the Sharpe ratio.
To test the sensitivity of the parameters chosen, we ran an parameter optimization job. We tested lookback periods of 2 trades to 50 trades in steps of 2 trades and we tested a scaling factor of ¼ (quarter Kelly) to 2 (double Kelly) in steps of ¼. Of the 200 parameter combinations, 77 (38.5%) had a greater return than the benchmark. The following images show the results of the parameter optimization:
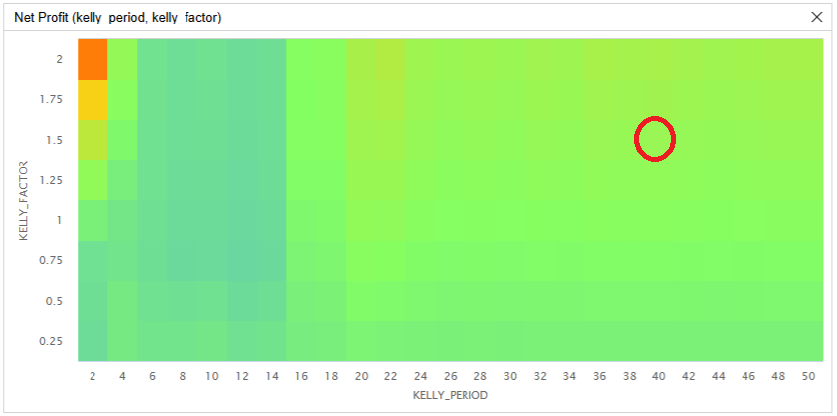
The red circle in the image above represents the parameter combination selected for the backtest in this post (40, 1.5). We chose these values because it's in an area on the x-axis where the performance is relatively stable and it's high enough on the y-axis to cause the portfolio to take on some leverage.






















Austin Kelly
Great research. Thank you. Thoughts on combining this with your Gradient Boosting Model? It seems reasonable that those two combined may provide improved stats?
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Rogelio espiritu
hi im not a programmer or coder but i want test live this trading strategy but i don't know how to change the 100k capital to 10k,happy new year!!
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Marc Daoust
Rogelio;
When you start the deployment, for paper trading (simulation/fake money), you enter your desired starting capital.
With real-money deployment, LEAN automatically obtains that amount from your broker.
Your algo's starting cash is used only when back-testing. Same for the Start and End dates.
Happy new year of coding!
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Rogelio espiritu
thanks for the reply and information
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
To unlock posting to the community forums please complete at least 30% of Boot Camp.
You can continue your Boot Camp training progress from the terminal. We hope to see you in the community soon!