Introduction
A Hidden Markov Model (HMM) estimates the probability an asset will continue similar behavior or jump to another state, making it a great tool to predict the current market regime (trending up, ranging, or trending down). In this micro-study, we implement a 3-component HMM strategy to detect market regimes and generate timely buy signals for liquid stocks on an intraday basis.
Background
A HMM is a probabilistic model representing a sequence of events or observations, where the underlying process that generates the observations is not directly observable.
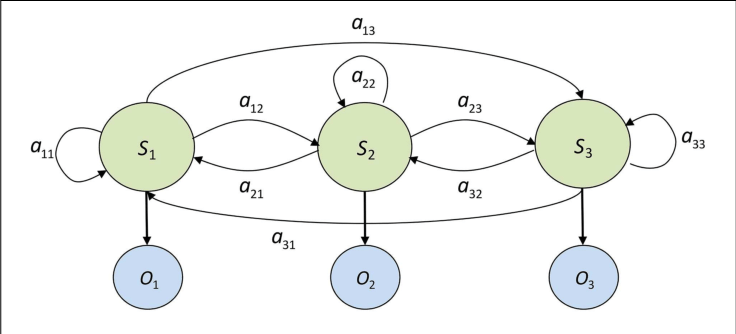
The use of HMMs in financial market analysis has gained traction in recent years. HMMs are powerful statistical models that can effectively capture the underlying, unobservable market states or "regimes" that drive asset price movements.
Their only input is price, so we wanted to focus on intraday timeframes to reduce the impact of the economy, politics and other macro factors. To start we chose 5-minute close price returns of the top 10 market cap stocks. These stocks tend to be highly liquid and less volatile, making them suitable for a rapid, intraday trading strategy. The 5-minute bar timeframe was sufficient to identify market regime shifts while maintaining a rapid response to intraday market fluctuations.
Implementation
To implement this on QuantConnect, we used universe selection, a data consolidator, and a returns indicator.
1. First, the strategy selects the top 10 US stocks by market capitalization. This is a fairly stable list as the top-10 don't change very frequently. By default this subscribes at minute resolution and updates daily.
def initialize(self):
self.add_universe(lambda fundamental: [f.symbol for f in sorted(fundamental, key=lambda x: x.market_cap, reverse=True)[:10]])2. We create a HMM object for the assets added to the algorithm, and set the random seed state to ensure the backtest result is repeatable. To remember the training state of the model we've created a model_month flag.
def on_securities_changed(self, changes):
for added in changes.added_securities:
added.model = hmm.GaussianHMM(n_components=3, n_iter=100, random_state=100)
added.model_month = -13. Then we consolidate the minute data, and pipe the 5-minute bars into the on_consolidated event handler. We also create the rate-of-change indicator which will record the history of returns for our model.
added.roc = RateOfChange(1)
added.roc.window.size = 150
added.consolidator = TradeBarConsolidator(timedelta(minutes=5))
added.consolidator.data_consolidated += self.on_consolidated
self.subscription_manager.add_consolidator(added.symbol, added.consolidator)4. Later, when five minute bars are produced, we update the RateOfChange indicator. This automatically adds new return values to its rolling window, building the training data for our model. When we have enough data, the model is trained on the points available.
def on_consolidated(self, _, bar):
security = self.securities[bar.symbol]
security.roc.update(bar.end_time, bar.price)
if security.roc.window.is_ready:
if security.model_month != bar.end_time.month:
security.model.fit(np.array([point.value for point in security.roc.window])[::-1].reshape(-1, 1))
security.model_month = bar.end_time.month5. The model can then use the latest 5-minute return to predict the current market regime for each asset. If P(positive) > P(negative), buy the stock, else short sell it. We use a fixed weight of 10% to ensure equal exposure.
post_prob = security.model.predict_proba(np.array([security.roc.current.value]).reshape(1, -1)).flatten()
self.set_holdings(bar.symbol, 0.1 if post_prob[2] > post_prob [0] else -0.1)Results
The implementation of a three-component Hidden Markov Model strategy for the top 10 market capitalization stocks yielded exceptional performance, with a Sharpe Ratio of 1.9. The model could quickly identify market regimes and capitalize on shifts in market conditions. By using a universe of liquid stocks we could efficiently trade intraday, and place multiple concurrent bets to smooth the overall return.

The algorithm parameter values (5, 150) were chosen at random. The strategy was resilient to a wide range of different parameters with all tests falling between 1.1-1.9 Sharpe Ratio.
As with any investment strategy, ongoing monitoring, optimization, and risk management practices are essential to maintain robust performance over time.
















Lee Ashley
Very nice
Remus Miclea
Thank for this, Louis, it got me started on the ML path, and look forward to learning more about it!
About the results: I cloned the code and checked the “baseline” results, given that the market was mostly in an uptrend, for the period considered (2023-Jan-01 till 2024-Sep-01, to be precise), and simply buying and holding could have been a successful strategy. To my surprise, I got better results, both as absolute return, as well as Sharpe ratio, when I forced the insights to be always UP (i.e. ignored any output of the HMM).
In other words, just buy-and-hold top 10 stocks, by market cap, outperforms the HMM model, for the said period. So, then, what is its value?
Piyush Ravi
Hey!I was wondering why did you choose “n_components=3”. I tried your code with with
“n_components = 2” and
“direction = InsightDirection.UP if post_prob[-1] > post_prob [0] else InsightDirection.DOWN”.
It was giving slightly better results.
Ross Bernstein
Could this be tested on a basket of futures?
Brandon Goyette
That would be interesting or maybe a basket of sector ETFs, across equities and maybe some with other less correlated exposures like a bitcoin ETF etc.
Kal Seehra
I played around with the asset selection a but and noticed that even in down markets, this HMM does not like to go short (typical short expose is less than 10%, even in a down market). Do you know why that would be? Is there a parameter that is biasing towards long exposure?
Louis Szeto
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
To unlock posting to the community forums please complete at least 30% of Boot Camp.
You can continue your Boot Camp training progress from the terminal. We hope to see you in the community soon!