Introduction
Technical analysis traders usually use graphical patterns to identify trading opportunities. Quant traders don't typically utilize these patterns in their automated trading systems because their presence is subjective, and they’re challenging to accurately detect. As a result, if these patterns have predictive power on future price movements, quant traders are missing an opportunity. To put it to the test, this tutorial explains a method to programmatically detect a popular graphical pattern in an event-driven trading algorithm. The results show that with just a simple time-based exit, the algorithm achieves greater risk-adjusted returns than the underlying benchmarks over the backtesting period.
Pattern Description
The pattern we use in this algorithm is the head and shoulders pattern, but this research can be extended to other graphical patterns. The head and shoulders pattern is characterized by two shoulders, a neckline, and a tall head in the middle.
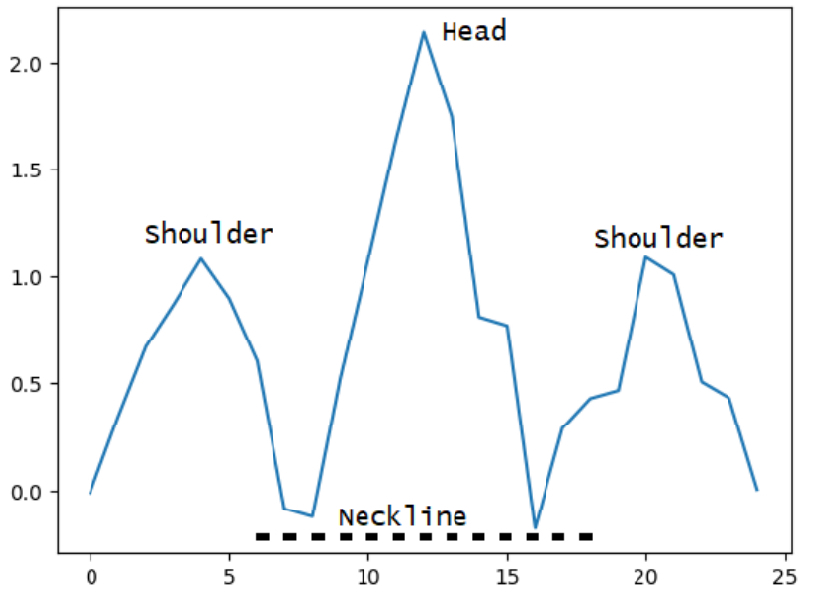
Some technical traders claim that the head and shoulders pattern signals an upcoming bullish-to-bearish trend reversal and that the neckline acts as a level of support.
Method
Let’s walk through how we can implement a head and shoulders trading algorithm with the LEAN trading engine.
Initialization
During initialization, we define some class variables, load all the algorithm parameters, and then add a coarse universe.
+ Expand
class HeadAndShouldersPatternDetectionAlgorithm(QCAlgorithm):trades = []new_symbols = []pattern_by_symbol = {}def initialize(self):self.set_start_date(2022, 1, 1)self.set_end_date(2023, 6, 1)self.set_cash(100000)# Pattern detection settingsself.window_size = self.get_parameter("window_size", 25)self.max_lookback = self.get_parameter("max_lookback", 50)self.step_size = self.get_parameter("step_size", 10)# Universe settingsself.coarse_size = self.get_parameter("coarse_size", 500)self.universe_size = self.get_parameter("universe_size", 5)# Trade settingsself.hold_duration = timedelta(self.get_parameter("hold_duration", 3))# Define universeself.universe_settings.resolution = Resolution.DAILYself.add_universe(self.coarse_filter_function)
Creating Pattern Detection Objects
We want to detect the presence of the head and shoulders pattern for as many securities as possible, so we scan for it once a day during universe selection. To ensure that we stay within the 10-minute quota for each step in the algorithm, we first reduce the number of coarse objects to only include the top 500 most liquid US Equities. Then, to enable us to scan for the pattern, we create HeadAndShouldersPattern objects for each US Equity in the subset of coarse objects.
+ Expand
def coarse_filter_function(self, coarse: List[CoarseFundamental]) -> List[Symbol]:coarse = sorted(coarse, key=lambda x: x.dollar_volume, reverse=True)[:self.coarse_size]# Create pattern detection objects for new securitiescoarse_symbols = [c.symbol for c in coarse]new_symbols = [symbol for symbol in coarse_symbols if symbol not in self.pattern_by_symbol]if new_symbols:history = self.history(new_symbols, self.max_lookback, Resolution.DAILY)for symbol in new_symbols:self.pattern_by_symbol[symbol] = HeadAndShouldersPattern(history.loc[symbol]['close'].values if symbol in history.index else np.array([]),self.window_size,self.max_lookback,self.step_size)# Remove pattern detection objects for delisted securitiesdelisted_symbols = [symbol for symbol in self.pattern_by_symbol.keys() if symbol not in coarse_symbols]for symbol in delisted_symbols:self.pattern_by_symbol.pop(symbol)# . . .
Generating Reference Patterns
To determine when the pattern occurs, we need to first generate many instances of the pattern. We need many unique samples to avoid a single, idealized pattern, so we add an element of randomness to each reference pattern. The following plot visualizes the data we generated:
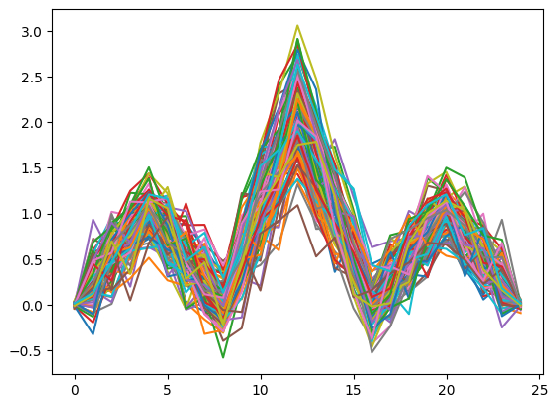
We generate this data during the construction of the first HeadAndShouldersPattern object and save it in a DataFrame as a static variable. The end of the constructor also scans the historical data sequence that we pass to the constructor to warm-up the detection system.
+ Expand
class HeadAndShouldersPattern(TechnicalPattern):def __init__(self, sequence, window_size, max_lookback, step_size):self.sequence = sequenceself.window_size = window_sizeself.max_lookback = max_lookbackself.step_size = step_size# Create pattern referencesif not hasattr(HeadAndShouldersPattern, "ref"):np.random.seed(1)ref_count = 100v1 = np.array([0] * ref_count) + 0.02 * norm.rvs(size=(ref_count, ))p1 = np.array([1] * ref_count) + 0.2 * norm.rvs(size=(ref_count, ))v2 = v1 + 0.2 * norm.rvs(size=(ref_count, ))v3 = v1 + 0.2 * norm.rvs(size=(ref_count, ))p3 = p1 + 0.02 * norm.rvs(size=(ref_count, ))p2 = 1.5 * np.maximum(p1, p3) + abs(uniform.rvs(size=(ref_count, )))v4 = v1 + 0.02 * norm.rvs(size=(ref_count, ))ref = pd.DataFrame([v1,(v1*.75+p1*.25) + 0.2 * norm.rvs(size=(ref_count, )),(v1+p1)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v1*.25+p1*.75) + 0.2 * norm.rvs(size=(ref_count, )),p1,(v2*.25+p1*.75) + 0.2 * norm.rvs(size=(ref_count, )),(v2+p1)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v2*.75+p1*.25) + 0.2 * norm.rvs(size=(ref_count, )),v2,(v2*.75+p2*.25) + 0.2 * norm.rvs(size=(ref_count, )),(v2+p2)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v2*.25+p2*.75) + 0.2 * norm.rvs(size=(ref_count, )),p2,(v3*.25+p2*.75) + 0.2 * norm.rvs(size=(ref_count, )),(v3+p2)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v3*.75+p2*.25) + 0.2 * norm.rvs(size=(ref_count, )),v3,(v3*.75+p3*.25) + 0.2 * norm.rvs(size=(ref_count, )),(v3+p3)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v3*.25+p3*.75) + 0.2 * norm.rvs(size=(ref_count, )),p3,(v4*.25+p3*.75) + 0.2 * norm.rvs(size=(ref_count, )),(v4+p3)/2 + 0.2 * norm.rvs(size=(ref_count, )),(v4*.75+p3*.25) + 0.2 * norm.rvs(size=(ref_count, )),v4])HeadAndShouldersPattern.ref = ((ref - ref.mean()) / ref.std()).T# Warm up the factor valuesself.rows = HeadAndShouldersPattern.ref.shape[0]self.scan()
Quantifying the Pattern Presence
After we create new HeadAndShouldersPattern objects for the new securities in the universe selection function, we update each object with their most recent price data.
def coarse_filter_function(self, coarse: List[CoarseFundamental]) -> List[Symbol]:# . . .for c in coarse:if c.symbol not in new_symbols:self.pattern_by_symbol[c.symbol].update(c.adjusted_price)# . . .
This update method updates the historical data in the HeadAndShouldersPattern objects and scans for patterns in the new data.
def update(self, price):self.sequence = np.append(self.sequence, price)[-self.max_lookback:]self.scan()
The scan method is where we quantify the presence of the pattern. This method calculates two factors for every security in the universe: correlation and Distance Time Warp (DTW) distance when compared to the reference patterns. It calculates these factors through the following procedure:
- Select lookback windows of varying lengths.
- Down-sample the lookback window to the same number of data points in the reference patterns, keeping the general shape but reducing the number of data points.
- Normalize the data in the trailing window.
- Calculate the correlation and DTW distance between the data in the trailing window and the data in each reference pattern.
- To aggregate the results into 2 factor values, take the max of the current factor value and the mean of the factor values across the reference patterns.
+ Expand
def scan(self):self.corr = 0self.similarity_score = 0# Select varying lengths of trailing windowsfor i in range(self.window_size, self.max_lookback, self.step_size):# Check if enough history to fill the trailing windowif len(self.sequence[-i:]) != i:break# Select the trailing data and downsample it to 25 data points# to match the number of data points in each reference pattern.# Downsampling allows us to detect the pattern across varying time scales,# large patterns and small patterns.sub_sequence = np.array(self.downsample(self.sequence[-i:], self.window_size))# Normalize the data in the trailing windowif sub_sequence.std() == 0:continuenorm_sub_sequence = (sub_sequence - sub_sequence.mean()) / sub_sequence.std()# Evaluate the pattern presence# Calculate correlation and similarity scores for each reference patterncorr_scores = np.ndarray(shape=(self.rows))similarity_scores = np.ndarray(shape=(self.rows))for j in range(self.rows):score, similarity = self.matching(norm_sub_sequence, self.ref.iloc[j, :])corr_scores[j] = scoresimilarity_scores[j] = similarity# After reviewing all of the reference patterns across varying lengths of lookback windows,# aggregate the results to produce a single value for each factor (correlation and similarity)self.corr = max(self.corr, corr_scores.mean())self.similarity_score = max(self.similarity_score, similarity_scores.mean())
The matching method applies a Savitzky-Golay filter to smooth the data in the lookback window and then calculates the DTW distance and correlation coefficient between the lookback window and the reference pattern.
class TechnicalPattern:def matching(self, series: np.array, ref: np.array) -> np.array:series_ = savgol_filter(series, 3, 2)series_ = (series_ - series_.mean()) / series_.std()path, similarity = dtw_path(ref, series_)series_ = np.array([series_[x[1]] for x in path])ref = np.array([ref[x[0]] for x in path])score = np.corrcoef(series_, ref)[0, 1]return score, similarity
To view the definition of the downsample method, see the technical_pattern.py file in the attached project.
The following image shows regions in a price series with high correlation and low DTW distance, which lead to a stronger head and shoulders signal. Note the varying sizes of the highlighted regions.
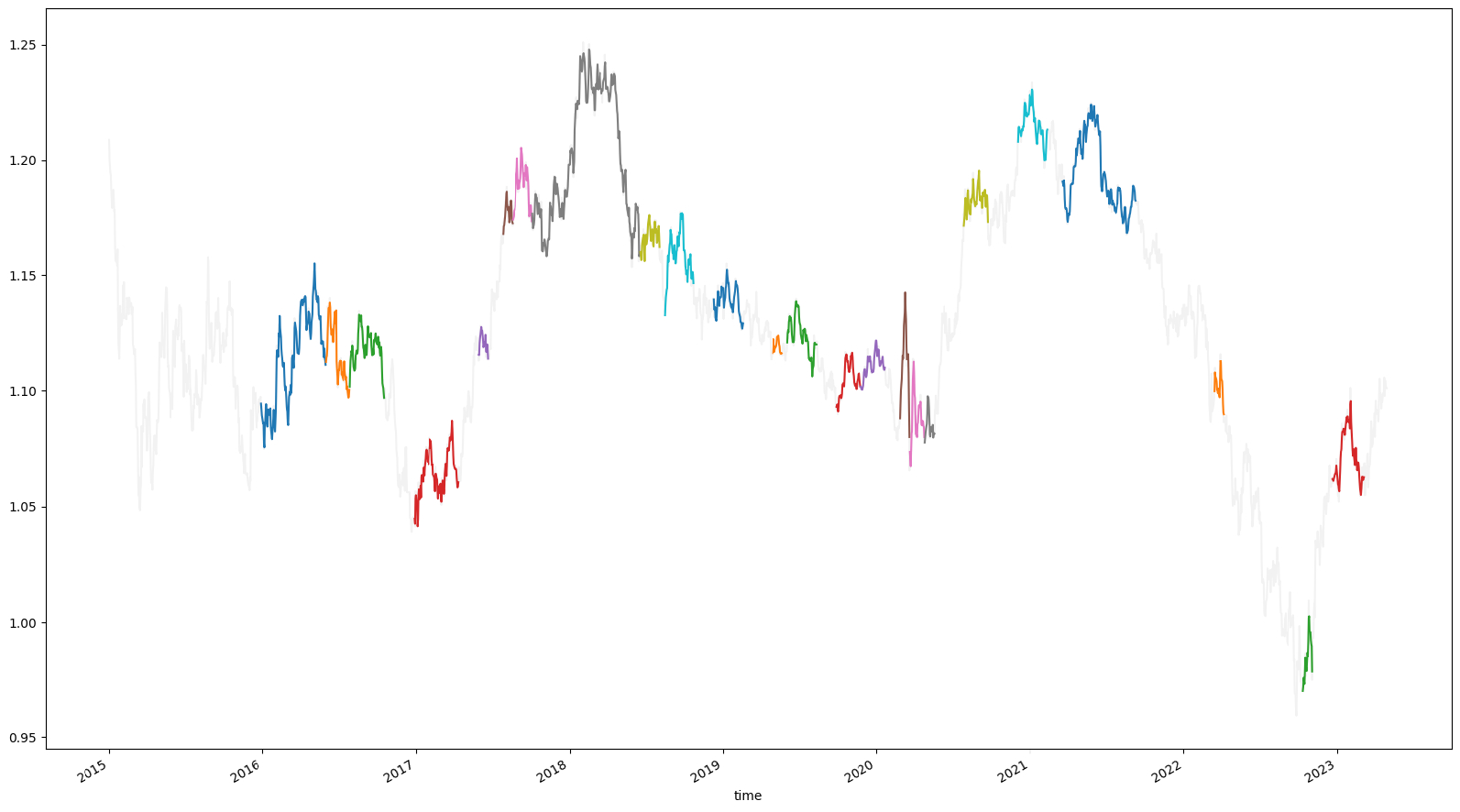
Selecting the Universe
We want the final universe to contain the securities that currently exhibit the clearest head and shoulders pattern. To this end, we define the universe selection function to select the 5 securities with the highest correlation and lowest DTW distance factor values.
def coarse_filter_function(self, coarse: List[CoarseFundamental]) -> List[Symbol]:# . . .# Step 1: Sort symbols by correlation in descending orderreverse_sorted_by_corr = [symbol for symbol, _ in sorted(self.pattern_by_symbol.items(), key=lambda x: x[1].corr, reverse=True)]# Step 2: Sort symbols by DTW distance in ascending ordersorted_by_dtw = [symbol for symbol, _ in sorted(self.pattern_by_symbol.items(), key=lambda x: x[1].similarity_score, reverse=False)]# Step 3: Add the ranks of each factor togetherrank_by_symbol = {symbol: reverse_sorted_by_corr.index(symbol)+sorted_by_dtw.index(symbol) for symbol in self.pattern_by_symbol.keys()}# Step 4: Select the symbols with the best combined rank across both factorsreturn [ symbol for symbol, _ in sorted(rank_by_symbol.items(), key=lambda x: x[1])[:self.universe_size] ]
Placing Trades
Since the head and shoulders pattern is a bearish signal for most technical traders, we define our trading rules to enter short positions when the pattern is detected and then sell a few days after the bearish signal has played out and the price decreased. The trading logic is as follows:
- Entry rule - When we first detect the pattern for a security (when the universe selection method selects a new security), short sell the security.
- Position sizing - $2,000 worth of shares
- Entry order type - Market order
- Exit rule - 3 days after entry
- Exit order type - Market order
To track when new securities first enter the universe, we take note of the new securities that are passed to the OnSecuritiesChanged method.
def on_securities_changed(self, changes):for security in changes.added_securities:if security.symbol not in self.new_symbols:self.new_symbols.append(security.symbol)
Then, to manage the trades, we define the OnData method to create new Trade objects for securities that just entered the universe and to destroy old Trade objects that have completed.
def on_data(self, data: Slice):# Short every stock when it first enters the universe (when we first detect the pattern)for symbol in self.new_symbols:self.trades.append(Trade(self, symbol, self.hold_duration))self.new_symbols = []# Scan for exitsclosed_trades = []for i, trade in enumerate(self.trades):trade.scan(self)if trade.closed:closed_trades.append(i)# Delete closed tradesfor i in closed_trades[::-1]:del self.trades[i]
The Trade class is where the algorithm actually places the orders.
+ Expand
class Trade:def __init__(self, algorithm, symbol, hold_duration):self.symbol = symbol# Determine position sizeself.quantity = -int(2_000 / algorithm.securities[symbol].price)if self.quantity == 0:self.closed = Truereturn# Enter tradealgorithm.market_order(symbol, self.quantity)self.closed = False# Set variable for exit logicself.exit_date = algorithm.time + hold_durationdef scan(self, algorithm):# Simple time-based exitif not self.closed and self.exit_date <= algorithm.time:algorithm.market_order(self.symbol, -self.quantity)self.closed = True
Results
We backtested the strategy from January 1, 2022 to June 1, 2023. The algorithm placed 1,817 trades and achieved a Sharpe ratio of 0.55. In contrast, buy-and-hold and short-and-hold for the SPY over the same time period achieved a Sharpe ratio of -0.179 and 0.409, respectively.
Further Research
If you want to continue developing this strategy, some areas of further research include:
- Testing other technical patterns
- Adjusting some of the algorithm parameters
- Trying new position sizing techniques for the entry order
- Adjusting position sizing throughout the trade as the factor values of the pattern fluctuate
- Trying new exit strategies
- Adding risk management
- Handling corporate actions

























Lucas Chan
Hi Derek,
10q for sharing this algo research. In the HeadAndShouldersPattern class initialisation, for the generation of the data points for the H&S object, any reason for you to use uniform.rvs for p2 value and norm.rvs for the rest of p & v values?
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Louis Szeto
Hi Lucas
The “p2” variable refers to the 2nd peak, the head part of the H&S pattern. For a valid H&S pattern, it must be higher than “p1”, so we deliberately use the uniform distribution to get
Regarding (2), it is worth noting that each possible case should be treated equally instead of emphasizing “more-likely" cases since we are doing detection but not time-series prediction. In fact, minority/marginal case training is even more valuable to a high-accuracy prediction model to differentiate" close case"!
Of course, there is no single way to produce the best training set, so we encourage you to share any thoughts/codes on improving the accuracy and spectrum of prediction.
Best
Louis
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Lucas Chan
Hi Louis,
Thank you for your input. I'm trying to run the code and understand it unfortunately, I got it run very slowly.Perhaps you can share how you & your team had run it efficiently. I am using compute node B2-8 and took I think 1-2hrs to run. Any recommendations for compute nodes upgrade?
Just by glancing the codes without more testings, I reckon that there's some improvement that can be done:
1. Risk management and stop loss with ATR factors.
2. The holding period of 3 days(?) is quite arbitrary, perhaps we can use the risk management model of Algo Framework(Migrating the above classic codes to algo framework)
3. More in-line comments/explanations in the codes will help….;)
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
Lucas Chan
To improve the execution times, I had replaced @jit with functools package.
Backtest Duration:
Sep'02 - Jun'03
Original time with @jit: 3323sec
Using functools package: 688secs
>> ~80% improvement in terms of execution time
Add this to the Head&ShouldersPattern
from functools import lru_cache
…..
…..
replace @jit with the following line…..
@lru_cache(maxsize=512)
Please help to share if there's an even better methods to improve run time. Tks.
The material on this website is provided for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation or endorsement for any security or strategy, nor does it constitute an offer to provide investment advisory services by QuantConnect. In addition, the material offers no opinion with respect to the suitability of any security or specific investment. QuantConnect makes no guarantees as to the accuracy or completeness of the views expressed in the website. The views are subject to change, and may have become unreliable for various reasons, including changes in market conditions or economic circumstances. All investments involve risk, including loss of principal. You should consult with an investment professional before making any investment decisions.
To unlock posting to the community forums please complete at least 30% of Boot Camp.
You can continue your Boot Camp training progress from the terminal. We hope to see you in the community soon!